Form 3 Mathematics

Chapter 4: Algebra 2

4.1. Introduction
4.2. Linear equations
4.2.1. Simple linear equations
4.2.2. Equations with fractions
4.3. Substitution of values
4.4. Changing the subject of the formula
4.4.1. Formula with brackets
4.4.2. Formula with squares and square roots
4.5. Simultaneous equations
4.5.1. Solving simultaneous equations by elimination
4.5.2. Solving simultaneous equations by substitution
4.6. Quadratic equations
4.6.1. Solving quadratic equations by factorisation
4.6.2. Solving quadratic equations using the perfect square case
4.6.3. Solving quadratic equations using the quadratic formula
4.7. Summary
4.8. Further reading
4.9. Test 4

4.1. Introduction

This chapter is a sequel to the topic on Algebra which you did in chapter 2.It seeks to equip you with the skills required in dealing with manipulation of algebraic equations, simultaneous equations and quadratic equations. You will realise that these skills are essential in solving numerous real life problems.

Objectives

After going through this chapter, you should be able to

  • solve different types of equations.
  • change the subject of a given formula.
  • substitute in a given formula.
  • solve both simultaneous and quadratic equations using different methods.
  • use the quadratic equation formula to solve quadratic equations.

Key terms

Equation – Is an algebraic statement that contains an equal sign.
Formula – A statement, especially an equation used to express a mathematical rule or principle.
Linear equation – It is a mathematical statement with an equal sign in which the highest power of the unknown is 1. For example 2x + 4 = 6, where x is the unknown and its power is 1.
Solve – Find the value of the unknown.
Subject of the formula – It is a variable which is expressed in terms of other variables involved in the formula.
Unknown – A letter in an equation, representing a number.
Variables – Letters that are used to represent numbers.

Time

You should not spend more than 10 hours in this chapter.

Study skills

You should have completed the chapter on Algebra 1 for you to undertake this chapter with ease. The key to mastery of mathematics is practice. You need to work out as many problems as possible about algebra to have a better understanding of the subject.

4.2. Linear equations

It is a mathematical statement with an equal sign in which the highest power of the unknown is 1. For example 2x + 4 = 6, where x is the unknown and its power is 1. There are basically two main classifications of linear equations. Some equations are regarded as simple linear equations while others are regarded as linear equations with fractions.

Note:

  • When an adding (or positive) number or value changes its side of the equal sign, it is subtracted or takes a negative value.
  • When a subtracting (or negative) number or value changes its side of the equal sign, it is added or takes a positive value.
  • When a multiplying number or value changes its side of the equal sign, it is divided.
  • When a dividing number or value changes its side of the equal sign, it is multiplied.

4.2.1. Simple linear equations

Linear equations are solved by collecting like terms together on the same side of an equal sign.

Example 1
Questions

  • If there are three people, Musa, Kuda and John. Let us say Musa is 𝑥𝑥 years old, Kuda is 5 years older than Musa, John is 3 times older than Kuda and the sum of their ages is 100. Find the ages of Musa, Kuda and John.

Answers

  • To find their ages you have to formulate an equation.
    let Musa’s age be x, Kuda’s age be x + 5 and John’s age will be 3(x + 5)
    the sum of their ages is
    x + x + 5 + (3x + 15)
    2x + 5 + 3x + 15
    5x + 20

    If the sum of ages is 100, then 5x + 20 = 100.
    5x + 20 = 100
    5x + 20– 20 = 100 − 20
    5x = 80
    \( \dfrac{5x}{5} = \dfrac{80}{5} \) (divide both sides by 5)
    x = 16
    Therefore Musa’s age is 16.

    Kuda’s age = x + 5
    = 16 + 5
    = 21
    Therefore Kuda’s age is 21.

    John’s age = 3(x + 5)
    = 3(16 + 5)
    = 3(21)
    = 63
    Therefore John’s age is 63.

Let us look at some more examples of linear equations.

Example 2
Questions

  • Solve the following linear equations.
    1. 5 – 2x = 7
    2. 3x – 5 = 7 – 4x
    3. 2m + 3 = 18 – 3m
    4. 4(3x – 2) – 3(2x – 1) = 7
    5. 6 – 4(2x – 3) = 2

Answers

  1. 5 – 2x = 7 (collect like terms)
    –2x = 7 – 5 (simplify)
    –2x = 2 (divide both sides by -2)
    \( \dfrac{−2x}{-2} = \dfrac{2}{-2} \)
    x = – 1
  2. 3x − 5 = 7 – 4x (collect like terms)
    3x + 4x = 7 + 5 (simplify)
    7x = 12 (divide both sides by 7)
    \( \dfrac{7x}{7} = \dfrac{12}{7} \)
    \( x = 1\dfrac{5}{7} \)
  3. 2m + 3 = 18 – 3m (collect like terms)
    2m + 3m = 18 – 3 (simplify)
    5m = 15 (divide both sides by 5)
    \( \dfrac{5m}{5} = \dfrac{15}{5} \)
    m = 3
  4. 4(3x – 2) – 3(2x – 1) = 7 (expand)
    12x – 8 – 6x + 3 = 7 (simplify)
    6x – 5 = 7 (collect like terms)
    6x = 7 + 5 (simplify)
    6x = 12 (divide both sides by 6)
    \( \dfrac{6x}{6} = \dfrac{12}{6} \)
    x = 2
  5. 6 – 4(2x – 3) = 2 (expand)
    6 – 8x + 12 = 2 (rearrange)
    –8x + 18 = 2 (collect like terms)
    –8x = 2 – 18 (simplify)
    – 8x = – 16 (divide both sides by 8)
    \( \dfrac{−8x}{8} = \dfrac{16}{8} \)
    x = 2

Hint: You can check the correctness of your answer by substituting the value of the unknown in the equation. For example, check weather x = 2 in question d.

  • 4(3x − 2) − 3(2x − 1) = 7
    4(3 × 2 − 2) − 3(2 × 2 − 1) = 7
    4(6 − 2) − 3(4 − 1) = 7
    4(4) − 3(3) = 7
    16 − 9 = 7
    7 = 7
L.H.S = R.H.S. Therefore the value of x is correct.

You may attempt the following exercise.

Exercise 4.1: Addition and subtraction of linear equations
Questions

  • Solve the following equations.
    1. 3x + 8 = 12 − 2x
    2. 2m + 12 − 5m = 7m − 8
    3. \( 3\dfrac{1}{2}m = 49 \)
    4. 12 − (3b + 5) = 16
    5. 3(3x − 2) − 4(5x − 1) = 0

Answers

  1. \( x = \dfrac{4}{5} \)
  2. m = 2
  3. m = 14
  4. b = −3
  5. \( -\dfrac{2}{11} \)

4.2.2. Equations with fractions

When solving equations with fractions you first need to clear the fractions by multiplying throughout by a common denominator (LCM) as shown in the following examples.

Example 3
Questions

  • Solve the following equations.
    1. \( \dfrac{2x + 1}{3} + \dfrac{x - 4}{5} = 2 \)
    2. \( \dfrac{4x - 1}{4} - 3\dfrac{1}{2} = \dfrac{2x + 3}{6} \)

Answers

  1. \( \dfrac{2x + 1}{3} + \dfrac{x - 4}{5} = 2 \) (find the LCM of 3, 5, 1 which is 15 and multiply each term by 15)
    \( \dfrac{15(2x + 1)}{3} + \dfrac{15(x - 4)}{5} = \dfrac{15(2)}{1} \) (simplify)
    5(2x + 1) + 3(x − 4) = 30 (expand)
    10x + 5 + 3x − 12 = 30 (collect like terms)
    10x + 3x = 30 + 12 − 5 (simplify)
    13x = 37 (divide both sides by 13)
    \( \dfrac{13x}{13} = \dfrac{37}{13} \)
    \( x = \dfrac{37}{13} \)
    \( x = 2\dfrac{11}{13} \)
  2. \( \dfrac{4x - 1}{4} - 3\dfrac{1}{2} = \dfrac{2x + 3}{6} \) (change \( 3\dfrac{}{} \) to an improper fraction)
    \( \dfrac{4x - 1}{4} - \dfrac{7}{2} = \dfrac{2x + 3}{6} \) (find the LCM of 2, 4, 6 which is 12 and multiply each term by 12)
    \( \dfrac{12(4x - 1)}{4} - \dfrac{12(7)}{2} = \dfrac{12(2x + 3)}{6} \) (simplify)
    3(4x − 1) − 6(7) = 2(2x + 3) (expand)
    12x − 3 − 42 = 4x + 6 (collect like terms)
    12x − 4x = 6 + 3 + 42 (simplify)
    8x = 51 (divide both sides by 8)
    \( \dfrac{8x}{8} = \dfrac{51}{8} \)
    \( x = \dfrac{51}{8} \)
    \( x = 6\dfrac{3}{8} \)

You may attempt the following exercise.

Exercise 4.1: Linear equations with fractions

  1. Solve the following equations.
    1. \( \dfrac{9x}{10} + \dfrac{2}{5} = \dfrac{2x}{5} + \dfrac{3}{10} \)
    2. \( \dfrac{3x + 4}{4} - \dfrac{x}{3} = \dfrac{2x - 1}{4} \)
    3. \( \dfrac{4}{5}(2x - 1) = \dfrac{2}{3}(2x + 5) + 1\dfrac{1}{3} \)
    4. \( \dfrac{x}{3} + 1\dfrac{1}{4}x + \dfrac{5}{12} = \dfrac{2x + 1}{4} \)
    5. \( \dfrac{4a - 1}{3} - \dfrac{3a - 1}{2} = \dfrac{a}{4} \)
  2. Formulate and solve equations on the following.
    1. Two farmers sold the same number of bags of maize. If farmer A harvested 120 bags and farmer B harvested 80 bags of maize. If the number of bags left by farmer A are twice the number of bags left by farmer B. Calculate the number of bags each sold.
    2. The sum of 8 and \( \dfrac{3}{5} \)of xproduces a result which is thrice x. Find the value of x.
    3. Peter and John shared $240. Peter got $30 more than John. Calculate John’s share.

Answers

    1. \( -\dfrac{1}{5} \)
    2. \( -2\dfrac{1}{7} \)
    3. \( 20\dfrac{1}{2} \)
    4. \( -\dfrac{2}{13} \)
    5. \( \dfrac{2}{5} \)
    1. 40
    2. \( 3\dfrac{1}{3} \)
    3. $105

4.3. Substitution of values

Substitution refers to putting values where the letters are. For example the formula for area of a trapezium = \( \dfrac{1}{2}(a + b)h \). It can be written as \( \dfrac{1}{2}(a + b)h \) h, where A (area) and a and b are parallel sides, then h the height of the trapezium. To find A the values of a, b and h should be given so that we substitute them in the formula.

Example 4
Questions

  • Given that \( A = \dfrac{1}{2}(a + b)h \), find A when a = 5cm, b = 11cm and h = 6cm.

Answers

  • \( A = \dfrac{1}{2}(a + b)h \) (substitute a, b and h)
    \( A = \dfrac{1}{2}(5 + 11)6 \)
    \( A = \dfrac{1}{2} \times 16 \times 6 \)
    \( A = 48cm^2 \)

Given a formula with unknown quantities, the other given quantities can be used to find the unknown quantity.

Example 5
Questions

  • If \( A = \dfrac{1}{2}bh \), find A when b = 8cm and h = 10cm.

Answers

  • \( A = \dfrac{1}{2}bh \) (substitute b and h)
    \( A = \dfrac{1}{2} \times 8 \times 10 \)
    \( A = 40cm^2 \)

There are instances where you may be given \( A = 30cm^2 \) and h = 10cm, and then tasked to find b. consider the following example.

Example 6
Questions

  • If \( A = \dfrac{1}{2}bh \), find b when \( A = 30cm^2 \) and h = 10cm.

Answers

  • \( A = \dfrac{1}{2}bh \) (substitute A and h)
    \( 30 = \dfrac{1}{2} \times b \times 10 \)
    \( 30 = 5b \)
    \( \dfrac{30}{5} = \dfrac{5b}{5} \)
    \( b = 6cm \)

Example 7
Questions

  • Given that \( I = \dfrac{P \times R \times T}{100} \).
    1. Find I when P = $560, R = 15% and T = 5 years.
    2. Find R when I = $450, P = $750 and T = 1.5 years.

Answers

  1. \( I = \dfrac{P \times R \times T}{100} \) (substitute P , R and T)
    \( I = \dfrac{560 \times 15 \times 5}{100} \)
    \( I = $420 \)
  2. \( I = \dfrac{P \times R \times T}{100} \) (substitute I , P and T)
    \( 450 = \dfrac{750 \times R \times 1.5}{100} \)
    \( 450 \times 100 = \dfrac{750 \times R \times 1.5}{100} \times 100 \)
    \( 45000 = 750 \times R \times 1.5 \)
    \( 45000 = 1125R \)
    \( \dfrac{45000}{1125} = \dfrac{1125R}{1125} \)
    \( R = 40 \)

You may attempt the following exercise.

Exercise 4.3: Substitution of values
Questions

  1. Given that \( A = \dfrac{1}{2}(a + b)h \).
    1. Find A, given that a = 7, b = 5 and h = 8.
    2. Find h, given that A = 40, a = 8 and b = 12.
  2. Given that C = 2πr.
    1. Find C, given that \( π = \dfrac{22}{7} \) and r = 14.
    2. Find r, given that \( π = \dfrac{22}{7} \) and C = 121.
  3. When calculating the wages of his workers, an employer uses the formula \( W = 250 + \dfrac{2T}{5} \) where W is the wage and T is overtime in hours.
    1. Calculate the wage if the employee had overtime of 20 hours.
    2. Calculate overtime if the employee got $360 as wages.

Answers

    1. 48
    2. 42
    1. 88
    2. 19.25
    1. 258
    2. 275

4.4. Changing the subject of the formula

Subject of the formula refers to a variable which is expressed in terms of other variables involved in the formula. For example, in the formula y = ax + b, ‘y’ is the subject. In order to make either a, or x, or b the subject, the formula has to be rearranged, as shown in the following examples.

Example 8
Questions

  • Make x the subject in the following equations.
    1. y = ax + b
    2. y = x + a
    3. y = x – a
    4. y = ax
    5. y = ax + bx

Answers

  1. \( y = ax + b \)
    \( y - b = ax \)
    \( \dfrac{y - b}{a} = x \)
    \( x = \dfrac{y - b}{a} \)
  2. y = x + a
    y - a = x
    x = y - a
  3. y = x – a
    y + a = x
    x = y + a
  4. \( y = ax \)
    \( \dfrac{y}{a} = x \)
    \( x = \dfrac{y}{a} \)
  5. \( y = ax + bx \)
    \( y = x(a + b) \)
    \( \dfrac{y}{a + b} = x \)
    \( x = \dfrac{y}{a + b} \)

4.4.1. Formula with brackets

When you want to change the subject of the formula where there are brackets, first remove the brackets.

Example 9
Questions

  • Make x the subject of the following.
    1. y = a(2 – x)

Answers

  1. \( y = a(2 – x) \)
    \( y = 2a - ax \)
    \( y + ax = 2a \)
    \( ax = 2a - y \)
    \( x = \dfrac{2a - y}{a} \)

4.4.2. Formula with squares and square roots

When you want to change the subject of the formula where there is a square root, first remove the square root by squaring both sides.

When you want to change the subject of the formula where a quantity is squared, first remove the square by finding the square root on both sides. Consider the following examples.

Example 10
Questions

  • Make 𝑥𝑥 the subject in the following.
    1. \( y = x^2 \)
    2. \( y = \sqrt{x} \)
    3. \( y = a\sqrt{x} \)
    4. \( y = a(x + b)^3 \)
    5. \( y = \sqrt{ax} \)

Answers

  1. \( y = x^2 \)
    \( \sqrt{y} = \sqrt{x^2} \)
    \( \sqrt{y} = x \)
    \( x = \sqrt{y} \)
  2. \( y = \sqrt{x} \)
    \( y^2 = (\sqrt{x})^2 \)
    \( y^2 = x \)
    \( x = y^2 \)
  3. \( y = a\sqrt{x} \)
    \( \dfrac{y}{a} = \sqrt{x} \)
    \( (\dfrac{y}{a})^2 = (\sqrt{x})^2 \)
    \( (\dfrac{y}{a})^2 = x \)
    \( x = (\dfrac{y}{a})^2 \)
  4. \( y = a(x + b)^3 \)
    \( \dfrac{y}{a} = (x + b)^3 \)
    \( ^3\sqrt{\dfrac{y}{a}} = ^3\sqrt{(x + b)^3} \)
    \( ^3\sqrt{\dfrac{y}{a}} = x + b \)
    \( ^3\sqrt{\dfrac{y}{a}} - b = x \)
    \( x = ^3\sqrt{\dfrac{y}{a}} - b \)
  5. \( y = \sqrt{ax} \)
    \( y^2 = (\sqrt{ax})^2 \)
    \( y^2 = ax \)
    \( \dfrac{y^2}{a} = x \)
    \( x = \dfrac{y^2}{a} \)

You may attempt the following exercise.

Exercise 4.4: Change of subject of formula
Questions

  • Make the letter in brackets the subject of the formula in each question.
    1. y = mx − b   (x)
    2. y = mx + bx   (x)
    3. ax + y = bx − 5   (x)
    4. y = a(a + bx)   (x)
    5. \( v = \dfrac{πr^2h}{3}   (r) \)
    6. \( v^2 = u^2 - 2as   (a) \)
    7. \( v = ut + \dfrac{1}{2}at^2 \)   (a)
    8. v = u + at   (t)
    9. \( m = \dfrac{b^2 + ax}{x + a}   (x) \)
    10. \( a = 2π\sqrt{\dfrac{h}{w}}   (w) \)
    11. \( m = \dfrac{b - n}{x}   (n) \)
    12. \( I = \dfrac{PRT}{100}   (t) \)
    13. \( \dfrac{1}{a} = \dfrac{1}{b} + \dfrac{1}{c}   (b) \)
    14. \( M = \sqrt{\dfrac{abx}{3 + y}}   (b) \)
    15. \( m = \dfrac{3p + 5}{x}   (p) \)

Answers

  1. \( x = \dfrac{y + b}{m} \)
  2. \( x = \dfrac{y}{m + b} \)
  3. \( x = \dfrac{y + 5}{b - a} \)
  4. \( x = \dfrac{y - a^2}{ab} \)
  5. \( r = \sqrt{\dfrac{3v}{πh}} \)
  6. \( a = \dfrac{u^2 - v^2}{2s} \)
  7. \( a = \dfrac{2(v - ut)}{t^2} \)
  8. \( t = \dfrac{v - u}{a} \)
  9. \( x = \dfrac{b^2 - ma}{m + a} \)
  10. \( w = \dfrac{4π^2h}{a^2} \)
  11. n = b – mx
  12. \( T = \dfrac{100I}{PR} \)
  13. \( b = \dfrac{ac}{c - a} \)
  14. \( b = \dfrac{m^2(3 + y)}{ax} \)
  15. \( p = \dfrac{mx - 5}{3} \)

Note: The expression ‘in terms of’ can be used in order for one to change the subject of the formula.

Example 11
Questions

  1. Given that y = ax – b write x in terms of y, a and b.
  2. Given that \( a = b\sqrt{c + 1} \), express c in terms a and b.

Answers

  1. \( y = ax – b \)
    \( y + b = ax \)
    \( \dfrac{y + b}{a} = x \)
    \( x = \dfrac{y + b}{a} \)
  2. \( a = b\sqrt{c + 1} \)
    \( \dfrac{a}{b} = \sqrt{c + 1} \)
    \( (\dfrac{a}{b})^2 = c + 1 \)
    \( \dfrac{a^2}{b^2} = c + 1 \)
    \( \dfrac{a^2}{b^2} - 1 = c \)
    \( c = \dfrac{a^2}{b^2} - 1 \)

4.5. Simultaneous equations

Simultaneous equations are equations that have two unknowns. For example,

  • 2x + 3y = 6
  • x – y = – 2

The unknowns in the simultaneous equations are x and y. Some of the methods used to solve simultaneous equations are elimination and substitution.

4.5.1. Solving simultaneous equations by elimination

This method involves eliminating one of the unknown by either subtracting or adding the two equations. Let us consider the following examples.

Example 12
Questions

  • Solve the following simultaneous equation by finding the values of x and y which satisfy both equations.
    1. x + y = 6
      x – y = 2
    2. 2x + 3y = 6
      x – y = –2

Answers

  1. x + y = 6   [1]
    x – y = 2   [2]

    To eliminate the variable y, we add equations 1 and 2.
    \( \begin{array}{r}\phantom{0}(x+y=6) \\ +(x-y=2) \\ \hline 2x+0=8 \end{array} \)
    \( 2x = 8 \)
    \( x = 4 \)

    To find the value of y, we substitute x = 4 into either equation 1 or 2.
    Substituting x = 4 into equation 1,
    4 + y = 6
    y = 6 – 4
    y = 2

    To check the correctness of the answer, the values of x and y are substituted into either equation 1 or 2. If the answer is correct, the left hand side of the chosen equation will be equal to the right hand side.
    Using equation 2,
    x – y = 2
    4 – 2 = 2
    2 = 2
    Therefore x = 4, y = 2.
  2. 2x + 3y = 6   [1]
    x – y = –2   [2]

    To eliminate the variable x, we multiply equation (2) by -2.
    -2(x – y = –2)
    -2x + 2y = 4
    Then add equations 1 and 2.
    \( \begin{array}{r}\phantom{0}(\phantom{0}2x+3y=6) \\ +(-2x+2y=4) \\ \hline 0+5y=10 \end{array} \)
    \( 5y = 10 \)
    \( y = 2 \)

    To find the value of y, we substitute y = 2 into either equation 1 or 2.
    Substituting y = 2 into equation 1,
    x – y = –2
    x – 2 = –2
    x = – 2 + 2
    x = 0

    To check the correctness of the answer, the values of x and y are substituted into either equation 1 or 2. If the answer is correct, the left hand side of the chosen equation will be equal to the right hand side.
    Using equation 2,
    x – y = –2
    0 – 2 = –2
    –2 = –2
    Therefore x = 0, y = 2.

4.5.2. Solving simultaneous equations by substitution

This method involves rearranging the equation to make the unknown the subject.

Example 13
Questions

  • Solve the following simultaneous equation by finding the values of x and y which satisfy both equations.
    • 2x + y = 5   [1]
      3x – 2y = 4   [2]

Answers

  • 2x + y = 5   [1]
    3x – 2y = 4   [2]
    Equation 1 can be rearranged to give,
    y = 5 – 2x

    This can then be substituted into equation 2.
    3x – 2(5 – 2x) = 4
    3x – 10 + 4x = 4
    3x + 4x = 4 + 10
    7x = 14
    x = 2

    To find the value of y, we substitute x = 2 into either equation 1 or 2.
    2x + y = 5
    2 (2) + y = 5
    4 + y = 5
    y = 5 – 4
    y = 1

    To check the correctness of the answer, the values of x and y are substituted into either equation 1 or 2. If the answer is correct, the left hand side of the chosen equation will be equal to the right hand side.
    Using equation 1,
    2x + y = 5
    2 × 2 + 1 = 5
    4 + 1 = 5
    5 = 5
    Therefore x = 2, y = 1.

You may attempt the following exercise.

Exercise 4.5: Simultaneous equations
Questions

  • Solve the following simultaneous equations using a suitable method.
    1. 4a + b = 14
      a + 5b = 13
    2. x + 2y = 8
      2x + 3y = 14
    3. 3c – d = 5
      2c + 5d = 9
    4. 3r + 2w = 2
      r + 5w = –8

Answers

  1. a = 3, b = 2
  2. x = 4, y = 2
  3. c = 2, d = 1
  4. r = 2, w = –2

4.6. Quadratic equations

A quadratic equation is an equation whereby the highest power of the unknown is 2, that is, the highest power of the variable x is \( x^2 \). The following are types of quadratic equations.

  • \( x^2 - 3x -10 = 0 \), \( 2y^2 - 13y + 15 = 0 \), \( m^2 - 8 = 0 \), \( 3r^2 + 4r + 1 = 0 \).

4.6.1. Solving quadratic equations by factorisation

The factorisation method can be used to solve quadratic equations as follows.

Example 14
Questions

  • Solve the following equations by factorising.
    1. \( x^2 - 5x = 0 \)
    2. \( x^2 + 10x + 25 = 0 \)
    3. \( x^2 + 2x - 24 = 0 \)
    4. \( 2x^2 + 11x + 12 = 0 \)
    5. \( 3x^2 + 7x - 6 = 0 \)

Answers

  1. \( x^2 - 5x = 0 \) (factorise)
    x(x - 5) = 0
    x = 0 or x – 5 = 0
    x = 0 or x = 5
  2. \( x^2 + 10x + 25 = 0 \)
    Find two values which multiply to give \( +25x^2 \), and add to give 10x from the factors of \( x^2 \) and 25.
    The only two values which satisfy both conditions are +5x and +5x.
    \( x^2 + 5x + 5x + 25 = 0 \)
    x(x + 5) + 5(x + 5) = 0
    (x + 5)(x + 5) = 0
    x + 5 = 0 or x + 5 = 0
    x = -5 or x = -5
    x = -5
  3. \( x^2 + 2x - 24 = 0 \)
    Find two values which multiply to give \( -24x^2 \), and add to give 2x from the factors of \( x^2 \) and -24.
    The only two values which satisfy both conditions are +6x and -4x.
    \( x^2 + 6x - 4x - 24 = 0 \)
    x(x – 4) + 6(x – 4) = 0
    (x + 6)(x – 4) = 0
    x + 6 = 0 or x – 4 = 0
    x = –6 or x = 4
  4. \( 2x^2 + 11x + 12 = 0 \)
    Find two values which multiply to give \( 24x^2 \) (2x × 12x), and add to give 11x from the factors of \( 2x^2 \) and 12.
    The only two values which satisfy both conditions are +8x and +3x.
    \( 2x^2 + 8x + 3x + 12 = 0 \)
    2x(x + 4) + 3(x + 4) = 0
    (x + 4)(2x + 3) = 0
    x + 4 = 0 or 2x + 3 = 0
    x = -4 or 2x = -3
    \( x = –4 \) or \( x = -\dfrac{3}{2} \)
  5. \( 3x^2 + 7x - 6 = 0 \)
    Find two values which multiply to give \( –18x^2 \) (3x × –6x), and add to give 7x from the factors of \( 3x^2 \) and -6.
    The only two values which satisfy both conditions are +9x and –2x.
    \( 3x^2 + 9x - 2x - 6 = 0 \)
    3x(x + 3) – 2(x + 3) = 0
    (x + 3)(3x – 2) = 0
    x + 3 = 0 or 3x – 2 = 0
    x + 3 = 0 or 3x = 2
    \( x = –3 \) or \( x = \dfrac{2}{3} \)

You may attempt the following exercise.

Exercise 4.6: Quadratic equations
Questions

  • Solve the following quadratic equations.
    1. \( x^2 + 7x + 10 = 0 \)
    2. \( a^2 - 8a + 12 = 0 \)
    3. \( 2x^2 - 3x - 2 = 0 \)
    4. \( 3b^2 + 10b - 8 = 0 \)
    5. \( x^2 - 36 = 0 \)
    6. \( 5m^2 - 2m = 0 \)
    7. \( x^2 + 6x + 9 = 0 \)
    8. \( 2x^2 + 3x + 1 = 0 \)
    9. \( 3x^2 - 27 = 0 \)
    10. \( m^2 = 8m \)

Answers

  1. –2 or –5
  2. 2 or 6
  3. \( 2 \) or \( -\dfrac{1}{2} \)
  4. \( -4 \) or \( \dfrac{2}{3} \)
  5. –6 or 6
  6. \( 0 \) or \( \dfrac{2}{5} \)
  7. –3 or –3
  8. \( -1 \) or \( -\dfrac{1}{2} \)
  9. –3 or 3
  10. 0 or 8

4.6.2. Solving quadratic equations using the perfect square case

Remember, if you are solving equations such as \( x^2= 9 \), you make ‘x’ the subject of the formula.

  • \( x^2 = 9 \)
    \( \sqrt{x^2} = \sqrt{9} \)
    \( x = ± \sqrt{9} \)
    \( x = ± 3 \)
    x = 3 or x = –3

Another type of equation \( (x + 3)^2 = 49 \) can be solved using the same method.

  • \( (x + 3)^2 = 49 \)
    \( \sqrt{(x + 3)^2} = ± \sqrt{49} \)
    \( x + 3 = ± 7 \)
    \( x = –3 ± 7 \)
    x = –3 + 7 or x = –3 – 7
    x = 4 or x = –10

Perfect squares

What is a perfect square? This is a number which can be written perfectly to the power of 2. For example \( 4 = 2^2 \) or \( 9 = 3^2 \). This is also applicable in quadratic expressions which are perfect squares, for example, \( x^2 + 6x + 9 = ( x + 3)^2 \).

Numbers such as 5 and 7 cannot be written perfectly to the power of 2. To write such numbers as 5 and 7 perfectly to the power 2, we express the number partly as a perfect square that is,

  • 5 = 4 + 1
    \( 5 = 2^2 + 1 \)

Where the quadratic is not a perfect square we make an effort to express it partly as a perfect square, for example,

  • \( x^2 + 4x + 7 \)
    \( x^2 + 4x + 2^2 - 2^2 + 7 \)
    \( (x^2 + 4x + 2^2) - 2^2 + 7 \)
    \( (x + 2)^2 + 3 \)
    Therefore \( x^2 + 4x + 7 = (x + 2)^2 + 3 \).

The following examples explain how to put a quadratic expression as a perfect square.

Example 15
Questions

  • Make the following expression perfect squares.
    1. \( a^2 + 8a \)
    2. \( x^2 - 10x \)

Answers

  1. \( a^2 + 8a \)
    Add a constant obtained by dividing the coefficient of ‘a’ by 2 and then square the result.
    \( a^2 + 8a + (\dfrac{8}{2})^2 \)
    \( a^2 + 8a + (4)^2 \)
    \( a^2 + 8a + 16 \)

    Now we have to factorise by looking for two values which multiply to give \( 16a^2 \), and add to give 8a from the factors of \( a^2 \) and 16. The numbers are +4a and +4a.
    \( a^2 + 4a + 4a + 16 \)
    a(a + 4) + 4(a + 4)
    (a + 4)(a + 4)
    \( (a + 4)^2 \)
  2. \( x^2 - 10x \)
    Add a constant obtained by dividing the coefficient of ‘x’ by 2 and then square the result.
    \( x^2 - 10x + (-\dfrac{10}{2})^2 \)
    \( x^2 - 10x + (-5)^2 \)
    \( x^2 - 10x + 25 \)

    Now we have to factorise by looking for two values which multiply to give \( 25x^2 \), and add to give -10x from the factors of \( x^2 \) and 25. The numbers are -5x and -5x.
    \( x^2 - 5x - 5x + 25 \)
    x(x - 5) - 5(x - 5)
    (x - 5)(x - 5)
    \( (x - 5)^2 \)

Example 16
Questions

  • Using the method of completing the square, solve
    1. \( a^2 + 6a + 7 = 0 \)
    2. \( x^2 + 3x - 2 = 0 \)

Answers

  1. \( a^2 + 6a + 7 = 0 \)

    Take 7 to the right side of the equation.
    \( a^2 + 6a = -7 \)

    Add the square of half the coefficient of ‘a’ on both sides
    \( a^2 + 6a + (\dfrac{6}{2})^2 = -7 + (\dfrac{6}{2})^2 \)
    \( a^2 + 6a + (3)^2 = -7 + (3)^2 \)
    \( a^2 + 6a + 9 = -7 + 9 \)
    \( a^2 + 6a + 9 = 2 \)

    Factorise the expression \( a^2 + 6a + 9 \) by looking for two values which multiply to give \( 9a^2 \), and add to give +6a from the factors of \( a^2 \) and 9. The numbers are +3a and +3a.
    \( a^2 + 3a + 3a + 9 = 2 \)
    a(a + 3) + 3(a + 3) = 2
    \( (a + 3)^2 = 2 \)

    The result produced on the left side is a perfect square \( (a + 3)^2 \) so you have to use the perfect square to complete the equation,
    \( a^2 + 6a + 9 = 2 \)
    \( (a + 3)^2 = 2 \)
    \( \sqrt{(a + 3)^2} = ± \sqrt{2} \)
    \( a + 3 = ± \sqrt{2} \)
    \( a = -3 ± \sqrt{2} \)
    \( a = -3 + \sqrt{2} \) or \( a = -3 - \sqrt{2} \)
  2. \( x^2 + 3x - 2 = 0 \)
    \( x^2 + 3x = 2 \)
    \( x^2 + 3x + (\dfrac{3}{2})^2 = 2 + (\dfrac{3}{2})^2 \)
    \( x^2 + 3x + (\dfrac{9}{4}) = 2 + (\dfrac{9}{4}) \)
    \( (x + \dfrac{3}{2})^2 = \dfrac{17}{4} \)
    \( \sqrt{(x + \dfrac{3}{2})^2} = ± \sqrt{\dfrac{17}{4}} \)
    \( x + \dfrac{3}{2} = ± \dfrac{\sqrt{17}}{4} \)
    \( x = -\dfrac{3}{2} ± \dfrac{\sqrt{17}}{4} \)
    \( x = \dfrac{-3 + \sqrt{17}}{2} \) or \( x = \dfrac{-3 - \sqrt{17}}{2} \)

Note: Usually the method of completing the square is done in equations that you cannot factorise.

You may attempt the following exercise.

Exercise 4.7: Completing the square
Questions

  • Use the method of completing the square to solve the following equations.
    1. \( x^2 + 2x - 2 = 0 \)
    2. \( x^2 - 8x + 1 = 0 \)
    3. \( a^2 + 5a + 2 = 0 \)
    4. \( m^2 - 5m + 2 = 0 \)
    5. \( p^2 + 8p + 15 = 0 \)

Answers

  1. \( -1 ± \sqrt{3} \)
  2. \( 4 ± \sqrt{15} \)
  3. \( \dfrac{-5 ± \sqrt{17}}{2} \)
  4. \( \dfrac{5 ± \sqrt{17}}{2} \)
  5. \( –3 \) or \( –5 \)

4.6.3. Solving quadratic equations using the quadratic formula

A quadratic equation takes the form \( ax^2 + bx + c = 0 \), where a, b and c are whole numbers. Quadratic equations can also be solved by the use of the quadratic formula which states that,

  • \( x = \dfrac{-b ± \sqrt{b^2 - 4ac}}{2a} \)

The following examples shows how to use the quadratic formula.

Example 17
Questions

  • Solve the following equations using the quadratic formula. Give your answers correct two decimal places.
    1. \( 13x^2 - 13x - 10 = 0 \)
    2. \( x^2 + 7x + 3 = 0 \)

Answers

  1. \( 13x^2 - 13x - 10 = 0 \)
    a = 3, b = –13 , c = –10

    Substitute the values in the quadratic formula.
    \( x = \dfrac{-(-13) ± \sqrt{(-13)^2 - 4 \times 3 \times -10}}{2 \times 3} \)
    \( x = \dfrac{13 ± \sqrt{169 - (-120)}}{6} \)
    \( x = \dfrac{13 ± \sqrt{169 + 120}}{6} \)
    \( x = \dfrac{13 ± \sqrt{289}}{6} \)
    \( x = \dfrac{13 ± 17}{6} \)
    \( x = \dfrac{13 + 17}{6} \) or \( x = \dfrac{13 - 17}{6} \)
    \( x = \dfrac{30}{6} \) or \( x = \dfrac{-4}{6} \)
    x = 5 or x = -0.67
  2. \( x^2 + 7x + 3 = 0 \)
    a = 1, b = 7 , c = 3

    Substitute the values in the quadratic formula.
    \( x = \dfrac{-7 ± \sqrt{7^2 - 4 \times 1 \times 3}}{2 \times 1} \)
    \( x = \dfrac{-7 ± \sqrt{49 - 12}}{2} \)
    \( x = \dfrac{-7 ± \sqrt{37}}{2} \)
    \( x = \dfrac{-7 ± 6.08}{2} \)
    \( x = \dfrac{-7 + 6.08}{2} \) or \( x = \dfrac{-7 - 6.08}{2} \)
    \( x = \dfrac{-0.92}{2} \) or \( x = \dfrac{-13.08}{2} \)
    x = -0.46 or x = -6.54

You may attempt the following exercise.

Exercise 4.8: Quadratic formula
Questions

  • Solve the following equations using the quadratic formula. Give your answers correct two decimal places.
    1. \( 2x^2 + 5x + 3 = 0 \)
    2. \( 5x^2 - 3x - 2 = 0 \)
    3. \( 3x^2 - 8x + 2 = 0 \)
    4. \( 4x^2 + 7x - 2 = 0 \)
    5. \( 5x^2 + 8x - 2 = 0 \)

Answers

  1. \( -1 \) or \( -\dfrac{3}{2} \)
  2. \( 1 \) or \( -\dfrac{2}{5} \)
  3. 2.3 or 0.28
  4. \( -2 \) or \( \dfrac{1}{4} \)
  5. 0.22 or -1.82

4.7. Summary

In this chapter, you have acquired the necessary skills that can help you in changing the subject of given formula, substitute in a given formula, solve both simultaneous and quadratic equations using different methods. Use these skills acquired to solve problems that you meet in other chapters.

4.8. Further reading

  1. Macrae, M. F., Madungwe, L. and Mutangadura, A. (2017). New General Mathematics Book 3. Pearson Capetown.
  2. Macrae, M. F., Madungwe, L. and Mutangadura, A. (2017). New General Mathematics Book 4. Pearson Capetown.
  3. Meyers, C., Graham, B., Dawe, L. (2004). Mathscape Working Mathematically. 9th Edition. MacMillan.
  4. Pimentel, R. and Wall, T. (2011). International Mathematics. Hodder UK.
  5. Rayner, D. (2005). Extended Mathematics. Oxford New York.

4.9. Test 4

Questions

    1. Solve 4(2x − 3) = 4.   [2]
    2. Given that a(bx - c) = y, make x the subject of the formula.   [3]
    1. Solve the equation \( \dfrac{3x - 8}{5} = 2 \).   [2]
    2. If \( \dfrac{ax + b}{c} = 2 \) write x in terms of a, b, c and y.   [3]
  3. A bank uses the formula \( S = a(1 + \dfrac{b}{100}) \) to calculate salaries of its workers.
    1. Calculate S when a = 900, b = 300.   [2]
    2. Make b the subject of the formula.   [3]
  4. Solve the equations.
    1. \( 3x^2 + 8x + 4 = 0 \)   [2]
    2. \( \dfrac{a - 1}{3} + \dfrac{2a - 3}{4} = \dfrac{5}{6} \)   [3]
  5. Solve the quadratic equation \( x^2 + 6x - 2 = 0 \) leaving answer to 2 decimal places.   [5]
  6. By connecting the 3 sides of the right-angled triangle

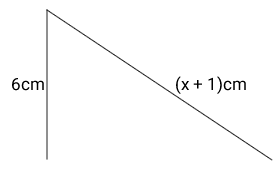
    Figure 4.1

    1. form an equation in terms of x in its simplest form.   [2]
    2. hence find the value of x.   [3]

Answers

    1. 2
    2. \( \dfrac{y - ac}{ab} \)
    1. 6
    2. \( x = \dfrac{cy - b}{a} \)
    1. 3600
    2. \( b = \dfrac{100S - 100a}{a} \)
    1. \( -2 \) or \( -\dfrac{2}{3} \)
    2. 2.3
  5. 0.32 or 6.32
    1. 4x = 36
    2. 9