Form 3 Mathematics
Chapter 3: Sets
3.1. Introduction
3.2. Set builder notation
3.3. Venn diagrams with two subsets
3.4. Venn diagrams with three subsets
3.5. Summary
3.6. Further reading
3.7. Test 3
3.1. Introduction
This chapter is a continuation of the topic on sets you did in Level 1. In this chapter you are going to learn about the set builder notation and how to use Venn diagrams to solve problems with at most three subsets.
Objectives
After going through this chapter, you should be able to
- define and describe set-builder notation by listing the elements.
- use Venn diagrams to show sets.
- use Venn diagrams to solve problems involving at most three sets and the universal set.
Key terms
Set – A set is a collection of different things; elements or members.
Set builder notation – It is a shorthand method of describing a set and it involves use of symbols to describe elements of a set as well as their properties.
Venn diagrams – This is another way of presenting sets using diagrams, a rectangle to represent universal set and circles to represent subsets.
Time
You should not spend more than 10 hours in this chapter.
Study skills
This topic builds on the topic of inequalities. This means that for you to easily understand the topic on sets, you should have gone through inequalities. The key to mastery of mathematics is practice. You need to work out as many problems as possible about sets to have a better understanding of the subject.
3.2. Set builder notation
A set builder notation is a shorthand method for describing sets and it involves the use of symbols to describe elements of a set as well as their properties. Remember set symbols at level 1. The following table shows the symbols, their meaning and use in the topic on sets.
Table 3.1: Set symbols
| Symbols | Meaning | Use |
|---|---|---|
| ξ or և | Universal set | ξ = { months of the year } |
| { - - - - } | A set of | W = { months of the winter } |
| ∈ | An element of | June = ∈ W |
| n(W) | Number of elements in set W | n(W) = 4 |
| ⊂ | Proper subset of | X ⊂ W |
| ⊆ | Improper subset of | If all elements of X are elements of W |
| ⊃ | X contains W | W ⊃ X |
| ∅ or { } | Empty or null set | A = ∅ |
| ∩ | Intersection or common element of two sets | A ∩ B |
| ∪ | Union of given sets, that is, all elements from the two sets | A ∪ B |
| W΄ | Complement of or not in the set | W΄ = { Nov, Dec, Jan } if W = {winter} then W΄ = {not winter} |
| N | Set of natural numbers | N = {1, 2, 3, ….} |
| Z | Set of integers | Z = {...,(-1), 0, (+1),...} |
| Q | Set of rational numbers | Q = \( {...,(–1\dfrac{1}{3}), (–0.6), \dfrac{1}{2}, 3, 14,...} \) |
Let us look at a few examples of what we did in Level 1 before we look into the set builder notation.
Example 1
Questions
-
State the meaning of the following.
- A ⊄ B, where A = {numbers}, B = {vowels}.
- 2 ∉ A, where A = {odd number}.
Answers
- A is not subset of B.
- 2 is not an element of set A.
In order for us to understand the set builder notation, we should be acquainted to the various ways in which information about sets is written down. Let us look into some few examples.
Example 2
Questions
-
Given that x ∈ N, list the members of the following sets.
- {x: x < 8}
- {x: x ≥ 4}
- {x: x ≤ 10}
Answers
-
Remember x ∈ N means that x is an element of natural members. Natural numbers are counting numbers from 1 to infinite (1, 2, 3,...).
- Therefore {x: x < 8} requires you to list counting numbers less than 8. In this case x is representing counting numbers: {1, 2, 3, 4, 5, 6, 7}.
- {x: x ≥ 4} this is a list of numbers, thus {4, 5, 6, 7...}. x is representing natural numbers from 4 to infinite where the three (3) dots (…) mean do not end.
- {x: x ≤ 10} = {1 ,2 ,3 ,4 ,5 ,6 ,7 ,8 ,9 10} or {1 ,2 ,3,...,8 ,9 ,10}. This is used when the elements (members) of the set are many but end. List the first three, put three dots and the last three. Another form of set builder notation is: a ∈ Z, meaning a is an element of a set of integers.
Note: Set of Z what is it? Check key words in Table 3.1.
Let us look at some more examples, and this time the set information is in a form of an equation.
Example 3
Questions
-
Given a ∈ Z, write down the elements of:
- a ∈ {a: 3a + 4 ≤ 10}
- a ∈ {a: < 3a + 1}
Answers
-
Z is a set of integers. Integers are {...,− 3, −2, −1, 0, 1, 2,...}. Therefore:
-
a ∈ {a: 3a + 4 ≤ 10}
3a + 4 ≤ 10
3a ≤ 10 − 4
3a ≤ 6
a ≤ 2
a = {2, 1, 0, −1,...} -
a ∈ {a: < 3a + 1}
16 < 3a + 1
16 − 1 < 3a
15 < 3a
5 < a or a > 5
a = {6, 7, 8, 9,...}
-
a ∈ {a: 3a + 4 ≤ 10}
Example 4
Questions
- If X ∈ Z, X = {x: x > −3} and Y = {x: x < 2}. List the elements X ∩ Y
Answers
-
X ∩ Y = {x: x > −3} ∩ {x: x < 2}
From X ∈ Z, X = {−2, −1, 0, 1, 2,...} and Y = {1, 0, −1, −2,...}
then X ∩ Y = {−1, −2, 0, 1}. These are the common elements of the two sets.
You may attempt the following exercise.
Exercise 3.1: Set builder notation
Questions
-
If X = {x: x is an integer, 1 < x ≤ 16}, Y = {even numbers}, Z = {perfect square}.
- List elements of set Y.
- List Y ∩ Z.
-
ξ = {x: 2 ≤ x ≤ 12, x ∈ N}, A = {x: x is a factor of 16}, B = {x: x is a prime number}.
- List the elements of set A.
- Find n (A ∪ B).
-
Given ξ = {1, 2, 3 … 18, 19, 20}. List the elements of each set.
- {x: x is an odd number, x ∈ ξ }.
- {x: x is a multiple of 3, x ∈ ξ }.
- {x: x − 6 > 10, x ∈ ξ }.
- {(x: y): y > 14 + x, x ∈ ξ, y ∈ ξ }.
- \( {(y: x): 4x^2 + 2, y ∈ ξ, x ∈ ξ } \).
- {(x: y): y is a cube of x, 4 ≤ y ≤ 20, 2 ≤ x ≤ 8}.
Answers
-
- {2, 4, 6, 8, 10, 12, 14, 16}
- {4, 16}
-
- {2, 4, 8}
- 7
-
- {1, 3, 5, 7, 9, 11, 13, 15, 17, 19}
- {3, 6, 9, 12, 15, 18}
- {17, 18, 19, 20}
- {(1;16), (1;17), (1;18), (1;19), (1;20), (2;17), (2;18), (2;19), (2;20), (3;18), (3;19), (3;20), (4;19), (4;20), (5;20)}
- {(1;6), (2;18)}
- {(2;8)}
3.3. Venn diagrams with two subsets
Venn diagrams can be drawn to represent any number of sets. Let us look at examples of questions which involve drawing of Venn diagrams with 2 subsets.
Example 5
Questions
- Out of 100 families 32 had radios and 51 had TV sets, if 40 had none of the two. How many had both?
Answers
-
Hint: Let x represent families with both radio and TV sets.
Let ξ = {100 families}
Let R = {families with radios}
Let T = {families with TV sets}
It is required to calculate n (R ∩ T)
Since n(R) = 32 – x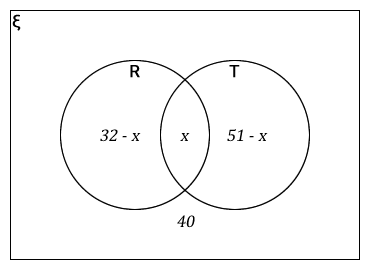
also n(T) = 51 – x, n(T ∩ R) = x and n(R΄ ∩ T΄) = 40
therefore 40 + (32 – x) + x + (51 – x) = 100
40 + 32 + 51 – x + x – x = 100
123 – x = 100
123 – 100 = x
23 = x
x = 23
Therefore 23 families have both radio and TV set.
Example 6
Questions
-
In the Venn diagram,
ξ = {farmers}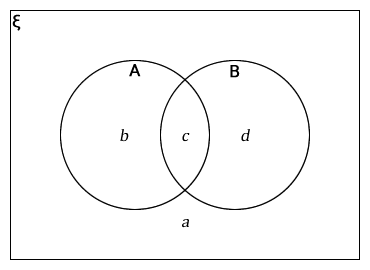
A = {animal rearing}
B = {crop farming}
The letters a, b, c, d represent the number of farmers in each subsets.
Given n(ξ) = 254, n(A) = 40 and n(B) = 30
- Express b in terms of c.
- Express d in terms of c.
- State the greatest possible value of c.
- Find the smallest possible value of a.
- Find a, b, d given that c = 4.
Answers
-
b + c = 40
b = 40 – c -
d + c = 30
d = 30 – c - c = 30
-
254 – (40 + 30)
254 – 70
184 (where c = 0) -
(b – c) + c + (d – c ) + a = 254
-
From (a),
b = 40 – c
b = 40 – 4
b = 36
therefore b = 36 -
From (b),
d = 30 – c
d = 30 – 4
d = 26
therefore d = 26 -
a + b + c + d = 254
a + 36 + 4 + 26 = 254
a + 66 = 254
a = 254 – 66
a = 188
therefore a = 188
-
From (a),
You may attempt the following exercise.
Exercise 3.2: Venn diagrams
Questions
-
Shade the following sets in the Venn diagram.
-
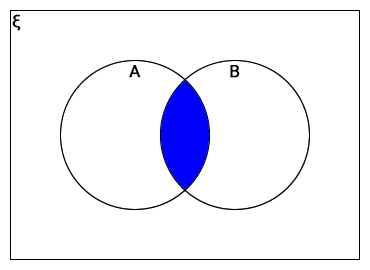
A ∩ B
-
X ∪ Y΄
-
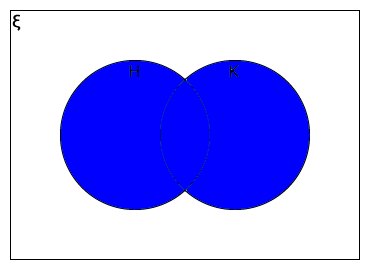
H ∪ K
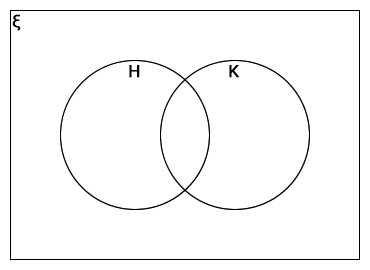
-
A ∩ B
-
List the elements of the following sets.
- {x ∶ x ≥ 6, x ∈ N}
- {x ∶ x ≤ 4, x ∈ Z}
- {x ∶ x < 8, x ∈ Z}
- {x ∶ x > −3, x ∈ Z}
-
Given ξ = {0, 1, 2, 3,..., 7, 8, 9}, list the elements:
- {x ∶ x = 2x + 3 ≤ 9, x ∈ ξ}
- {(x, y) ∶ y = x + 4, x ∈ ξ, y ∈ ξ}
-
ξ = {x ∶ 1 ≤ x < 15, x is an integer}
A = {x ∶ x is a multiple of 3}
B = {x ∶ x even numbers}
List members of each set:- A = { }
- B = { }
- A ∩ B = { }
Answers
-
-
A ∩ B
-
X ∪ Y'
-
H ∪ K
-
A ∩ B
-
- {6, 7, 8,...}
- {..., 2, 3, 4}
- {..., 5, 6, 7}
- {-2, -1, 0,...}
-
- {0, 1, 2, 3}
- { 0,4 }{ 1,5 }{ 2,6 }{ 3,7 }{ 4,8 }{5,9 }
-
- A = {3, 6, 9, 12}
- B = {2, 4, 6, 8, 10, 12, 14}
- A ∩ B = {6, 12}
3.4. Venn diagrams with three subsets
It is very important to identify each set in ξ.
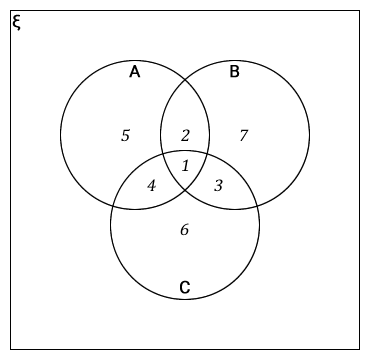
Regions: 1 = A ∩ B ∩ C = all 3 sets
Regions: 2 = A ∩ B = A & B only
Regions: 3 = B ∩ C = B & C only
Regions: 4 = A ∩ C = A & C only
Regions: 5 = A only
Regions: 6 = C only
Regions: 7 = B only
Once you understand the different regions in a set, and you are able to place information in the correct set, then it should be easy for you to solve problems involving three subsets.
Example 7
Questions
-
At a school there are 10 boys. 6 study History, 5 study Bible and 7 study Maths, 3 study History and Bible, 2 study Bible and Maths and 4 study History and Maths. Each boy does at least one of the three subjects. How many boys do all three subjects? Use first letter of each subject to group the boys:
H = {boys who study History}
B = {boys who study Bible}
M = {boys who study Maths}
all 10 boys form your universal set (ξ)
ξ = {all 10 boys}
Answers
-
Let x be boys how do all 3 subjects.
At the centre that is where you put x meaning all the three subjects. History and Bible (H ∩ B) is where you place 3 – x, Bible and Maths (B ∩ M) you place 2 – x and History and Maths (H ∩ M), you place 4 – x.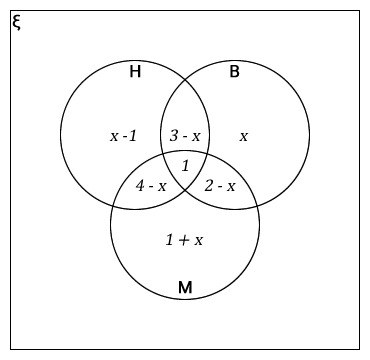
-
Those doing History only are:
6 – (3 – x) – x – (4 – x)
6 – 3 + x – x – 4 + x
6 – 7 + x, which is x – 1. -
Those doing Bible only are:
5 – (3 – x) – x – (2 – x)
5 – 3 + x – x – 2 + x
5 – 5 + x, which is x. -
Those doing Maths only are:
7 – (4 – x) – x – (2 – x)
7 – 4 + x – x – 2 + x
7 – 6 + x, which is 1 + x.
Hint: Take note of boys who do one subject are worked out first. Now all sets or subsets are filled with appropriate information.
-
So,
(x – 1) + (3 – x) + x + x + (2 – x) + (x + 1) + (4 – x) = 10
since H ∪ B ∪ M = ξ,
simplifying our equation and solving for x thus,
x – 1 + 3 – x + x + x + 2 – x + x + 1 + 4 – x = 10
4x – 3x – 1 + 10 = 10
x + 9 = 10
x = 10 - 9
x = 1
Therefore only 1 boy does all three subjects.
You may attempt the following exercise.
Exercise 3.3: Venn diagrams with three subsets
Questions
-
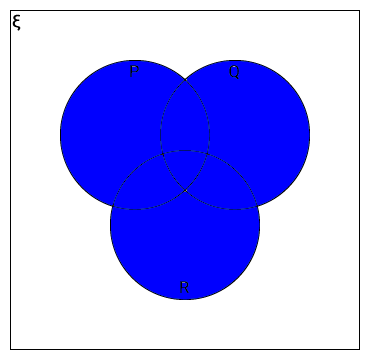
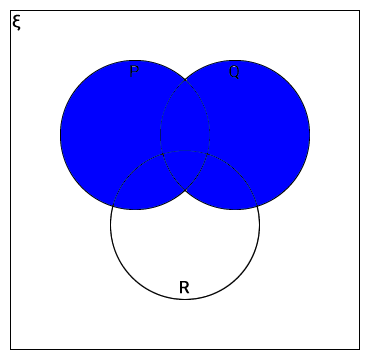
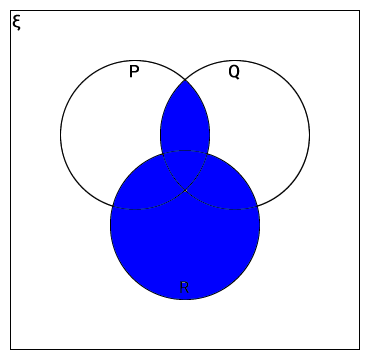
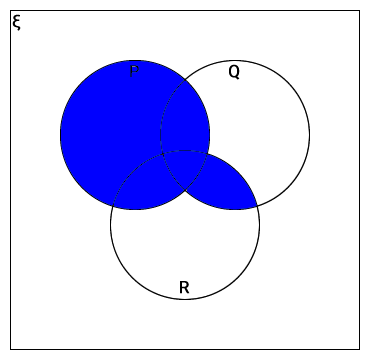
Shade the following sets in the Venn diagram.
- P ∩ Q ∩ R
- P ∪ Q ∪ R
- (P ∪ Q) ∩ R
- (P ∩ Q) ∪ R
- P ∪ (Q ∩ R)
- Q΄ ∩ ( P ∪ R)
- P΄ ∪ ( Q ∩ R)
- Q΄ ∩ ( P ∩ R)
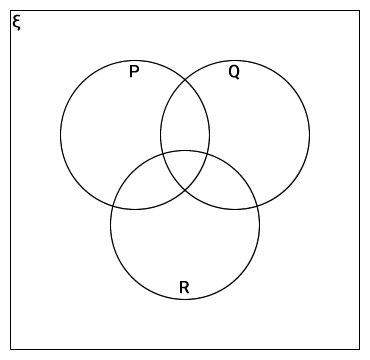
-
If in a group of learners, 24 play Handball, 28 play Baseball and 21 play Softball. 8 play Handball only, 14 play Baseball only and 7 play Handball and Baseball only and 4 play Baseball and Softball only. How many play:
- All three games?
- Handball and Softball only?
- Softball only?
- If 10 play none, how many learners are at the school?
Answers
-
-
P ∩ Q ∩ R
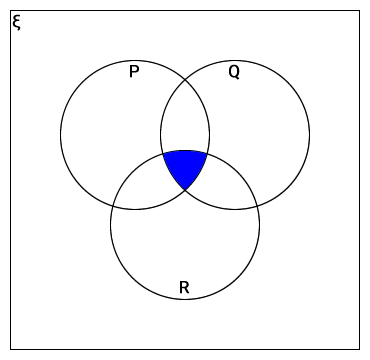
-
P ∪ Q ∪ R
-
(P ∪ Q) ∩ R
-
(P ∩ Q) ∪ R
-
P ∪ (Q ∩ R)
-
Q΄ ∩ ( P ∪ R)
-
P΄ ∪ ( Q ∩ R)
-
Q΄ ∩ ( P ∩ R)
-
P ∩ Q ∩ R
-
In the diagram,
ξ = {all learners}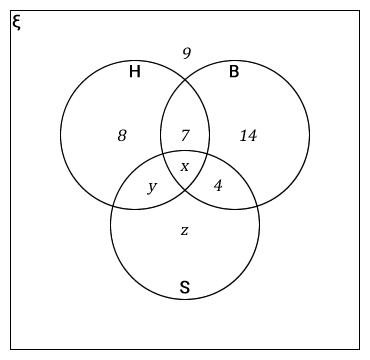
H = {Handball}
B = {Baseball}
S = {Softball}
Note: Start by finding x since those who play baseball = 28-
Hence,
x = 28 – (7 + 14 + 4)
x = 28 – 25
x = 3
Therefore 3 play all the three games. -
y represent those who play handball and softball. Since those who play handball are 24 you can find y thus,
y + 8 + x + 7 = 24
y + 8 + 3 + 7 = 24
y + 18 = 24
y = 24 – 18
y = 6
Therefore 6 play handball and softball only. -
If those who play softball are 21 then,
x + 4 + y + z = 21
3 + 4 + 6 + z = 21
13 + z = 21
z = 21 – 13
z = 8
Therefore those who play softball only are 8. -
8 + 7 + 14 + 4 + 3 + 6 + 8 + 10 = 60
Therefore the total number of learners is 60.
-
Hence,
x = 28 – (7 + 14 + 4)
You may attempt the following exercise.
Exercise 3.4: Solving problems involving sets
Questions
-
The Venn diagram shows elements in their appropriate regions.
If n(ξ) = 42, calculate the following.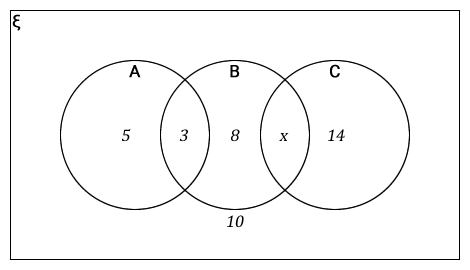
- X
- n(B)
- n(A ∪ C)
- n(A ∩ C)
- n(C΄ ∩ B΄)
- n(A΄ ∪ B)
-
The Venn diagram shows sets H and K.
State: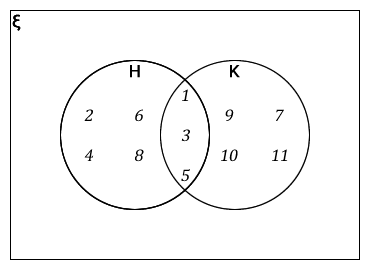
- n(H ∩ K)
- n(H ∪ K)
- H΄
- (H ∪ K)΄
-
In a group of drivers, 40 like fish, 31 like beef and 45 like chicken. 10 like fish only, 15 like beef only and 20 like chicken and fish. If 14 like fish and beef, and 6 like beef and chicken.
-
Calculate how many like
- Chicken only?
- All three dishes?
- How many drivers were there?
-
Calculate how many like
Answers
-
-
10 + 5 + 3 + 8 + x + 14 = 42
40 + x = 42
x = 42 – 40
x = 2 -
n(B) = 3 + 8 + 2
= 13 -
n(A ∪ C) = (5 + 3) + (2 + 14)
= 8 + 16
= 24 - n(A ∩ C) = 0 (There are no common elements for set A and set C, i.e., they are disjoint sets.)
-
n(C΄ ∩ B΄) = 5 + 10
= 15 -
n(A΄ ∪ B) = 8 + 10 + 14 + 2
= 34
-
10 + 5 + 3 + 8 + x + 14 = 42
-
- n(H ∩ K) = 3
- n(H ∪ K) = 11
- H΄ = {7, 9, 10, 11}
- (H ∪ K)΄ = { } (There are no elements outside the two sets. This is a null set.)
-
In the diagram,
let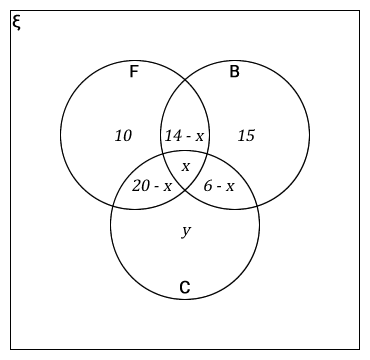
F = {drivers who like fish}
B = {drivers who like beef}
C = {drivers who like chicken}
Hint: Note the word only. This will help you to identify sets as shown in the diagram above, and let those who like chicken only be y. Those who like fish and beef may like chicken too, this is why 14 – x and those who like beef and chicken might like fish.-
You should start by calculating x, taking those who like beef or fish:
Beef => (14 – x) + x + (6 – x) + 15 = 31
14 – x + x + 6 – x + 15 = 31
15 + 14 + 6 – x = 31
35 – x = 31
x = 35 – 31
x = 4
or Fish => 10 + (14 – x) + x + (20 – x) = 40
10 + 14 – x + x + 20 – x = 40
44 – x = 40
x = 44 – 40
x = 4- Therefore those who like all three dishes are 4.
-
Those who like chicken only are:
(20 – x) + x + (6 – x) + y = 45
20 – x + x + 6 – x + y = 45
20 – 4 + 4 + 6 – 4 + y = 45
20 + 6 – 4 + y = 45
22 + y = 45
y = 45 – 22
y = 23
Therefore 23 drivers like chicken only.
-
10 + 10 + 4 + 16 + 2 + 15 + 23 = 80
Therefore the total numbers of drivers is 80.
-
You should start by calculating x, taking those who like beef or fish:
3.5. Summary
In this chapter you have learnt about sets, set builder notations, Venn diagrams with two, and three subsets, and the application of Venn diagrams in solving real-life problems.
3.6. Further reading
- Macrae, M. F., Madungwe, L. and Mutangadura, A. (2017). New General Mathematics Book 3. Pearson Capetown.
- Macrae, M. F., Madungwe, L. and Mutangadura, A. (2017). New General Mathematics Book 4. Pearson Capetown.
- Meyers, C., Graham, B., Dawe, L. (2004). Mathscape Working Mathematically. 9th Edition. MacMillan.
- Pimentel, R. and Wall, T. (2011). International Mathematics. Hodder UK.
- Rayner, D. (2005). Extended Mathematics. Oxford New York.
3.7. Test 3
Questions
-
Given
ξ = {x: 0 ≤ x < 100, x is an integer}
M = {x: x is a multiple of 4}
P = {x: x is a perfect square}- List the elements of M. [2]
- List the elements of P. [2]
- Find n(M ∩ P). [1]
- List the elements of (M ∪ P). [1]
- Find n(M ∪ P). [1]
-
Given
ξ = {x: x < 15, x ∈ Z } (consider positive integers only)
A = {even number}
B = {odd number}
C = {3, 6, 9, 12}
Find- n (B ∩ C) [2]
- A' [2]
- (A ∩ C)' [2]
- (B ∪ C) [2]
-
If ξ = {1, 2, 3, . . . 18, 19, 20} , list the members of the following sets.
- {x: x + 2 > 16 } [2]
- {(x, y): y = 15 + x, y ∈ ξ, x ∈ ξ} [3]
- {(x, y): y = 3x7 – 5, x ∈ ξ, y ∈ ξ} [3]
-
54 girls chose a drink each with at least one of the following flavours.
The Venn diagram represents the number of girls in the subsets.
Guava (G)
Peach (P)
Apple (A)
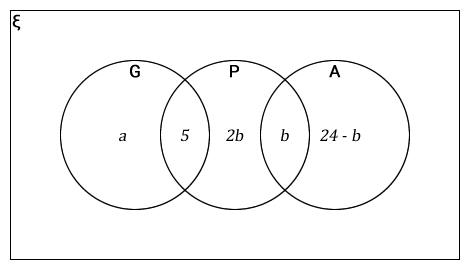
- Write down the total number of girls who chose apple.
- Express a in terms of b in its simplest form.
-
Girls who chose apple only were 3 more than those whose who chose peach only.
- Write an equation in b.
- Solve your equation.
- Calculate the number of girls who chose peach only.
Answers
-
- M = {4, 8, 12, 16, 20, 24, 28, 32, 36, 40, 44, 48, 52, 56, 60, 64, 68, 72, 76, 80, 84, 88, 92, 96}
- P = {1, 4, 9, 16, 25, 36, 49, 64, 81}
- 4
- {4, 8, 9, 12, 16, 20, 24, 25, 28, 32, 36, 40, 42, 44, 48, 49, 52, 56, 60, 64, 68, 72, 76, 80, 81, 84, 84, 88, 92, 96}
- 31
-
- 2
- {1, 3, 5, 7, 9, 11, 13}
- {1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14}
- {1, 3, 5, 6, 7, 9, 11, 12, 13}
-
- {15, 16, 17, 18, 19, 20}
- {(1, 16), (2, 17), (3, 18), (4, 19), (5, 20)}
- (2, 7)
-
- 24
- a = 25 – b
-
- 2b + 3 = 24 - b
- b = 7
- 14
