Form 3 Mathematics

Chapter 10: Geometry 3

10.1. Introduction
10.2. Similarity
10.3. Scale Factor
10.4. The Area Factor
10.5. The Volume Factor
10.6. Summary
10.7. Further Reading
10.8. Test 10

10.1. Introduction

This chapter will dwell much on the similarity ratios of areas and volumes. This concept is a derivative of similarity and congruency covered at level 1. Various examples will be used to simplify the concept for you. The assessment section will also contain typical examination question papers. You are also expected to recall the calculation of volumes of solid shapes.

Objectives

After going through this chapter, you should be able to

  • calculate the scale factors.
  • calculate the area of plane and solid shapes.
  • calculate the volume factors of plane and solid shapes.

Key terms

Equiangular - refers to similar triangles, equal in angle sizes, but different in size of the shapes.
Similar - objects are similar if they show equivalency in characteristics except for size.

Time

You should not spend more than 8 hours in this chapter.

Study skills

The key to mastery of mathematics is practice. You need to work out as many problems as possible about geometry to have a better understanding of the subject.

10.2. Similarity

Two polygons are said to be similar if

  1. they are equi-angular, and
  2. the corresponding sides are in proportion.
For triangles, being equi-angular implies that corresponding sides are in proportion. The converse is also true.

10.3. Scale Factor

This concept was well covered at level 1 and the following example serves as a reminder of the concept and this will assist you to understand the area and volume factors quite easily.

Example 1
Questions

  • The diagrams show two similar shapes.

    Figure 10.1

    Calculate the scale factor.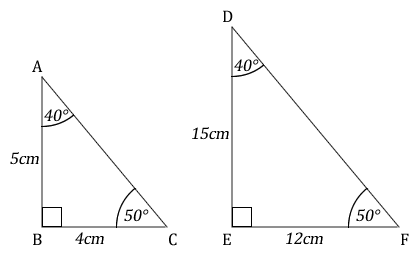

Answers

The triangles given are equiangular, that means they are similar and their scale factor can be found using the following formula.

  • Scale factor = ratio of the corresponding sides
    \( Scale factor = {{15} \over {5}} = 3 \), or
    \( Scale factor = {{12} \over {4}} = 3 \)

10.4. The Area Factor

The ratio of the areas of two similar shapes or figures is the square of the scale factor of the two shapes.

Example 2
Questions

  • The diagram shows two similar shapes.

    Figure 10.2

    Calculate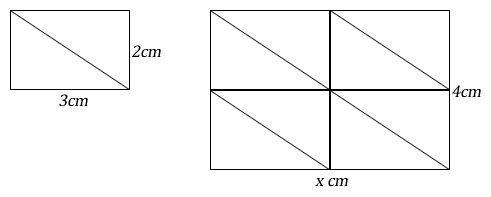
    1. the scale factor,
    2. the value of x,
    3. the area factor.

Answers

  1. \( \dfrac{4}{2} = 2 \)
  2. \( \dfrac{x}{3} = \dfrac{4}{2} \)
    \( x = 3 \times {{4} \over {2}} = 6 \), or x = 3 × scale factor = 3 × 2 = 6
  3. \( \dfrac{Area \space of \space big \space rectangle}{Area \space of \space small \space rectangle} = \dfrac{6 \times 4}{3 \times 2} = \dfrac{24}{6} = 4 \), or
    \( (scale factor)^2 = (2)^2 = 4 \)

Example 3
Questions

  • Area A has an area of \( 12m^2 \) and a similar area B has an area of \( 1.5m^2 \). If area A has one of its dimension equal to 310cm. Find the corresponding dimension of area B.

Answers

Area factor of area B to area A = \( {{1.5} \over {12}} = {{1} \over {8}} \)
Scale factor = square root of area factor = \( \sqrt{{1} \over {8}} \)
Length of dimension A = 310cm
Length of dimension B = scale factor × dimension A
= \( \sqrt{\dfrac{1}{8}} \times 310 \)
= \( \dfrac{1 \times 310}{\sqrt{8}} \)
= 109.6 (3 s.f.)

Note: Examiners are also interested in scale drawing and map interpretation, therefore we need to do an example of that nature.

Example 4
Questions

  • A map is drawn to a scale of 1:25500. Find the area in hectares of an irrigation field which has an area of \( 20cm^2 \). Hint: 1ha = \( 10000m^2 \).

Answers

Scale factor = 25500
Area factor = \( (25500)^2 = 650250000 \)
Irrigation field = \( 650250000 \times 20cm^7 \)
= \( \dfrac{650250000 \times 20}{100 \times 100}m^2 \)
= \( \dfrac{650250000 \times 20}{10000 \times 100 \times 100}ha \)
= 130.05ha

You may attempt the following exercise.

Exercise 10.1: Area of similar shapes
Questions

  1. The diagrams show two similar triangles with corresponding sides in the ratio 3:5.

    Figure 10.3

    Find the ratio of their areas.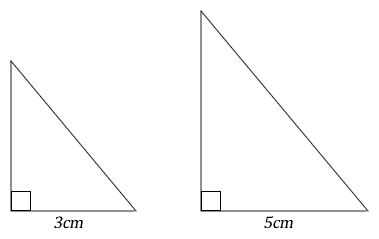
  2. In the diagram, triangles ABC and BDC are right angled.

    Figure 10.4

    1. State in correct order the two triangles similar to triangle DCB.
    2. Find
      1. the side DC,
      2. the scale factor of triangle ABC and BDC,
      3. the area factor of triangles stated in (ii).
  3. The diagram shows two right angled triangles where straight lines BD and AC intersect at X.

    Figure 10.5

    Calculate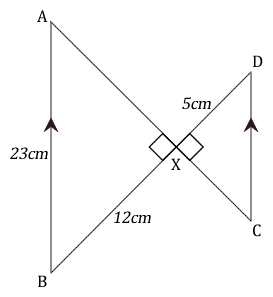
    1. the areas of the two triangles,
    2. the area factor of the larger triangle to the smaller one.
  4. Two pentagons have corresponding sides of 3cm and 7cm. Find
    1. the ratio of their areas,
    2. the area of the smaller pentagon, if the area of the larger one is \( 350m^2 \),
    3. the area of the larger pentagon, if the area of the smaller one is \( 133m^2 \).
  5. The ratio of the area of two circles is \( 3 \over 4 \). Find
    1. the ratio of their radii,
    2. the radius of the smaller circle, if the radius of the larger one is 24cm,
    3. the radius of the larger circle, if the radius of the smaller one is 15cm.
  6. A cultivated land covers an area of 8 hectares. Find the area in \( cm^2 \) of the cultivated land when drawn on a map of scale 1:50000.
  7. The area of the window pane of a sliding door is \( 3m^2 \). In a reduced photograph of the house, the window pane is a rectangle of 10cm by 2cm. Find the length and breadth of the real window pane.
  8.  

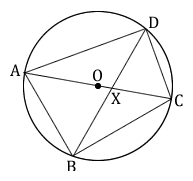
    Figure 10.6

    1. Write down the triangle that is similar to triangle AXB.
    2. If \( {{AD} \over {DX}} = {{3} \over {2}} \), find the ratio \( {{Area \space of \space triangle \space BAX} \over {Area \space of \space triangle \space DCX}} \)

Answers

  1. 25:9
    1. DBA and BCA
      1. 3
      2. 2:1
      3. 4:1
    1. 20.4 and 117.7
    2. 144:25
    1. 9:49
    2. 64.3
    3. 124.1
    1. \( \sqrt{3}:2 \)
    2. \( 12\sqrt{3} \)
    3. \( 10\sqrt{3} \)
  6. \( 0.32cm^2 \)
  7. \( 2\sqrt{1500}cm \times 10\sqrt{1500} \)
  8. xxx

10.5. The Volume Factor

The ratio of the volumes of the similar solids is the cube of the scale factor of the similar solids. The diagram shows two similar solid cylinders, one of height 6h and radius 3r, the other of height 3h and radius r.

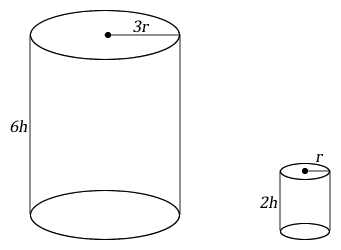
Figure 10.7

The heights and radii are of the same ratio and it shows that the shapes are similar.

The scale factor of the small cylinder to the large cylinder = \( 2h \over 6h \), or \( r \over 3r \) = \( 1 \over 3 \).

Remember, volume of a cylinder = \( πr^2h \).

Volume factor of the small cylinder to the big cylinder
= ratio of volumes
= \( \dfrac{πr^2(2h)}{π(3r)^2(6h)} = \dfrac{2}{9 \times 6} = \dfrac{1}{27} = (\dfrac{1}{3})^2 \)

Example 5
Questions

  • Two similar conical containers contain 135ml and 320ml of cough syrup respectively.

    Figure 10.8

    If the vertical height of 135ml of syrup is 6cm, find the vertical height of 320ml of syrup.

Answers

Capacity is proportional to volume, thus, ratio of volumes
= ratio of capacity
= \( \dfrac{135}{320} = \dfrac{27}{64} = \dfrac{3^3}{4^3} = (\dfrac{3}{4})^3 \)

Scale factor = \( 3 \over 4 \)
Height of 135ml = 6cm
Height of 320ml = \( {4 \over 3} \times 6 = 8cm \)

You may attempt the following exercise.

Exercise 10.2: Volumes of similar shapes
Questions

  1. Two similar tanks are 42m and 28m high respectively. If the larger tank holds 12000 litres of water. Find the capacity of the smaller one.
  2. An architect designs a scale model of a building. The volumes of air in the scale model and the actual building are \( 30000m^3 \) and \( 220m^3 \). If the height of the window in the actual building is 4.8m, find the height of the door in the scale model.
  3. An ice-cream cone costs $2. How much would a similar ice-cream cone, 4 times the height and diameter cost?
  4. The diagram shows two similar frustums with capacities of 27 litres and 8 litres respectively.

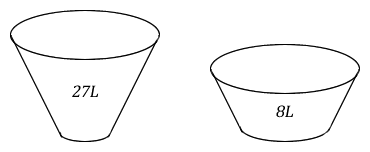
    Figure 10.9

    Find
    1. the ratio of heights,
    2. the height of the larger frustum if the smaller one is 36cm high.
  5. Two circular holes are similar in shape and have diameters of 10cm and 30cm. If water is poured into the holes, find
    1. the ratio of their heights,
    2. the capacity in litres of the larger hole if the smaller hole holds 2litres when full.
  6. Two bolts are similar in shape and have radii of 1,2mm and 4.8mm.
    1. Find the ratio of their masses.
    2. If the mass of the larger bolt is 30g, find the mass of the larger bolt.

Answers

  1. 3555.6
  2. 0.933
    1. 3:2
    2. 121.5
    1. 1:3
    2. 54
    1. \( 1 \over 64 \)
    2. 1920
    1. xxx
    2. xxx

10.6. Summary

In this chapter we made it simple for you to understand the concept of area factors and volume factors by revisiting the aspect of similarity in some of our examples. Various examples have been included to prepare you for examination questions in the test section. Try to refer to the given examples where you encounter advanced questions in the test section.

10.7. Further Reading

  1. Macrae, M. F., Madungwe, L. and Mutangadura, A. (2017). New General Mathematics Book 3. Pearson Capetown.
  2. Macrae, M. F., Madungwe, L. and Mutangadura, A. (2017). New General Mathematics Book 4. Pearson Capetown.
  3. Meyers, C., Graham, B., Dawe, L. (2004). Mathscape Working Mathematically. 9th Edition. MacMillan.
  4. Pimentel, R. and Wall, T. (2011). International Mathematics. Hodder UK.
  5. Rayner, D. (2005). Extended Mathematics. Oxford New York.

10.8. Test 10

Questions

  1. Given that AE = 8cm, BD = 2.5cm, CE = 6cm and the area of triangle BCD = \( 24cm^2 \),

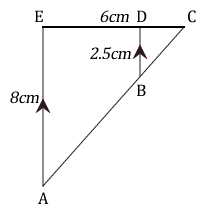
    Figure 10.10

    Find
    1. two similar triangles,
    2. the scale factor and area factor of the two similar triangles,
    3. the area of the trapezium ABDE.
  2. In the diagram PQ:PR = 2:5, the area of triangle QRS is \( 15cm^2 \).

    Figure 10.11

    Find the area of triangle PRS.
  3. In the diagram, PQ is parallel to UV, PQ = 9cm, UV= 6cm and VR = 8cm.

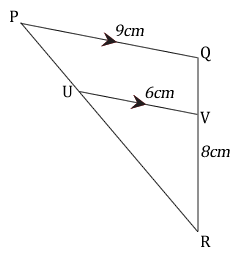
    Figure 10.12

    1. Name, in correct order the triangle which is similar to triangle VUR.
    2. Calculate VQ.
    3. Given that the area of triangle VUR = \( 32cm^2 \), calculate the area of the trapezium PUVQ.
  4. In the diagram, BP = BQ, PBA = CBQ and BAQ = BCP.

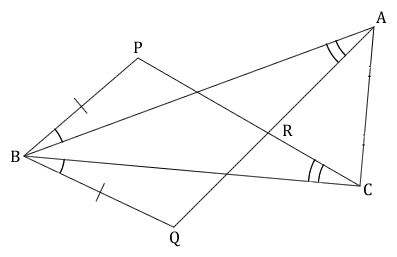
    Figure 10.13

    1. Name, in correct order, the triangle that is congruent to triangle ABQ. State the case of congruency.
    2. Hence write down pairs of equal elements, not already given, in the congruent triangles.
  5. In the diagram, SR is parallel to PQ, and SQ and PR intersect at T.

    Figure 10.14

    Given that PT = 10cm, RT = 2,5cm, and PQ = 16cm, calculate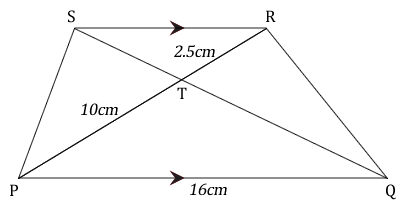
    1. SR,
    2. the ratio of the area of triangle RTS to the area of triangle PTQ,
    3. the ratio of the area of triangle PTQ to the area of triangle QTR.
  6. In the diagram, PQRS is a parallelogram. X is a point on PS produced such that PX= 3PS and the area of the parallelogram is \( 12cm^2 \).

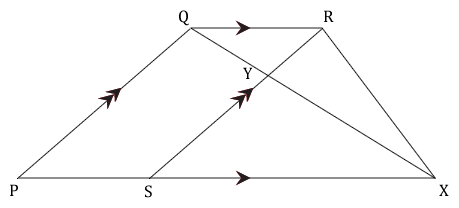
    Figure 10.15

    1. Find the area of triangle QRX.
    2. Calculate the following ratios giving your answers as common fractions in their lowest terms:
      1. \( \dfrac{QR}{SX} \)
      2. \( \dfrac{the \space area \space of \space ΔQRY}{the \space area \space of \space ΔXYS} \)
  7. Two circles have areas of \( 6{1 \over 4}m^2 \) and \( 2{1 \over 2}m^2 \) respectively.
    1. Express the area of the smaller circle as a percentage of the area of the larger circle.
    2. Calculate the ratio \( radius \space of \space the \space larger \space circle \over radius \space of \space the \space larger \space circle \) leaving your answer in surd form.
    3. (In this part, take π to be \( 22 \over 7 \)
      Calculate the radius of the larger circle.
  8. In the diagram, M is the midpoint of CD.

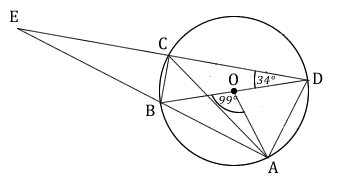
    Figure 10.16

    1. Explain why triangle OMD is similar to triangle BCD.
    2. Write down the value of \( area \space of \space ΔOMD \over area \space of \space ΔBCD \)
  9. In the diagram, triangle AQR is similar to triangle ABC.

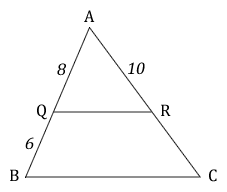
    Figure 10.17

    1. Calculate the length of RC.
    2. Given that the area of triangle AQR is \( 32cm^2 \), calculate the area of triangle ABC.
  10. A, B, C, D and E are five different shaped blocks of ice in a refrigerated room.
    1. At 11 p.m. on Monday the cooling system failed, and the blocks started to melt.
      At the end of each 24 hour period, the volume of each block was 12% less than its volume at the start of that period.
      1. Block A had a volume of \( 7500cm^3 \) at 11 p.m. on Monday.
        Calculate its volume at 11 p.m. on Wednesday.   [2]
      2. Block B had a volume of \( 6490cm^3 \) at 11 p.m. on Tuesday.
        Calculate its volume at 11 p.m. on the previous day.   [2]
      3. Showing your working clearly, find on which day the volume of Block C was half its volume at 11 p.m. on Monday.   [2]
    2. [The volume of a sphere is \( {4 \over 3}πr^3 \).]
      [The surface area of a sphere is \( 4πr^2 \).]
      At 11 p.m. on Monday Block D was a hemisphere with radius 18cm.
      Calculate
      1. its volume,   [2]
      2. its total surface area.   [2]
    3. As Block E melted, its shape was always geometrically similar to its original shape. It had a volume of \( 5000cm^3 \) when its height was 12cm.
      Calculate its height when its volume was \( 1080cm^3 \).   [2]