Form 3 Mathematics

Chapter 1: Real Numbers

1.1. Introduction
1.2. Number concepts and operations
1.3. Ratios, rates and proportions
1.4. Irrational numbers
1.5. Approximations, estimations and limits of accuracy
1.6. Ordinary and standard form
1.7. Number bases
1.8. Scale and simple map problems
1.9. Number patterns and sequences
1.10. Summary
1.11. Further reading
1.12. Test 1

1.1. Introduction

This chapter seeks to identify the different types of real numbers with special reference to rational and irrational numbers. This chapter is also going to look at how to add, subtract, multiply and divide real numbers that you meet in your daily situations.

Objectives

After going through this chapter, you should be able to

  • distinguish between rational and irrational numbers.
  • perform operations involving real numbers.
  • solve problems involving distance and area using scale.
  • convert a number in one base to the other.
  • solve equations involving number bases.
  • identify missing numbers in a sequence.

Key terms

Binary – Means base 2.
Denary – Means base 10.
Irrational numbers – These are numbers that cannot be written as exact fractions, for example \( \sqrt{2} \), \( \sqrt{3} \) or π.
Rational numbers – These are numbers that can be written as fractions, for example \( \dfrac{3}{4} \), \( \dfrac{5}{2} \), 0.75 or \( \dfrac{a}{b} \).
Sequence – A set of numbers with a well-defined order or pattern, for example {2, 4, 6, 8} or {1, 4, 9}.
Standard form – This involves writing a number in the form \( A \times 10^n \), where A is a number between 1 and 10, while n is a positive or negative whole number (integer).

Time

You should not spend more than 10 hours in this chapter.

Study skills

The key to mastery of mathematics is practice. You need to work out as many problems as possible about real numbers to have a better understanding of the subject.

1.2. Number concepts and operations

What is a number?

A number is a way to represent quantity. Numbers are not something that you can touch or hold, because they are not physical. When we look at the world around us, we quantify it using numbers. For example, we may say:

  • How many learners?
  • How much money?
  • How much distance?

These are some of the questions which can only be answered using numbers. A number can be written in many different ways and it is always advisable to choose the most appropriate way of writing the number. For example, ‘a quarter’ may be spoken aloud or written in words. It can also be written as a fraction or as a decimal number 0.25.

Real numbers

These are numbers found on a number line, both negative and positive numbers. Now that we have learnt about what a number is, we can look at what real numbers are in greater detail. The following are examples of real numbers and it is seen that each number is written in a different way:

  • \( \sqrt{6} \), 2.45434, \( \dfrac{5}{2} \), π, –22, \( - \dfrac{15}{7} \), –14.3

From the following list, identify real numbers in the space provided.

  • \( 1\dfrac{9}{5} \), 6k, \( - \dfrac{1}{2} \), –9, 3x, 4z, 2π, 7, \( \dfrac{x}{3} \)

Hint: If you have chosen numbers without letters you got it right.

Depending on how the real number is written, it can be further labelled as either rational, irrational, integer or natural.

Natural numbers

The first type of numbers that are learnt about are the numbers that are used for counting. These numbers are called natural numbers and are the simplest numbers in mathematics:

  • 1, 2, 3, 4,...

Mathematicians use the symbol ℕ to mean the set of all natural numbers. These are also called positive whole numbers. The natural numbers are a subset or part of the real numbers since every natural number is also a real number.

Integers

Integers are positive and negative whole numbers:

  • ...,−4, −3, −2, −1, 0, 1, 2, 3, 4,...

Mathematicians use the symbol ℤ to mean the set of all integers. The integers are a subset of real numbers, since every integer is a real number.

Rational numbers

Natural numbers and integers are only able to describe quantities that are whole or complete. For example you can have 4 apples, but what happens when you divide one apple into 4 equal parts and share it among your friends? Then it is not a whole apple anymore and a different type of number is needed to describe the apples. This type of number is known as a rational number.

A rational number is any number which can be written as \( \dfrac{a}{b} \), where a and b are integers and b ≠ 0.

The following are examples of rational numbers:

  • \( \dfrac{7}{3}, - \dfrac{1}{2}, \dfrac{60}{20}, \dfrac{7}{21}, \dfrac{10}{1}, 11 \)

From the following list, identify rational numbers in the space provided.

  • 5, \( - \dfrac{5}{3} \), - 9, \( \dfrac{17}{19} \), π, \( \dfrac{10}{1} \)

Mathematicians use the symbol ℚ to mean the set of all rational numbers. A rational number may be a proper or improper fraction.

Irrational numbers

An irrational number is any real number that cannot be expressed as an exact fraction. Irrational numbers when expressed as decimals, they can never be fully written out as they have an infinite number of decimal places which never fall into a repeating pattern. Pi(π) is a unique example of an irrational number. You may argue that π can be written as \( \dfrac{22}{7} \), but this value of π is merely an approximate value of π. That is why we tend to classify π under irrational numbers.

For example,

  • \( \sqrt{2} = 1,41421356... \)
  • \( π = 3.14159265... \)

You may attempt the following exercise.

Exercise 1.1: Rational and Irrational numbers
Questions

  1. List any 5 examples of rational numbers between 2 and 3.
  2. From the list of numbers below identify rational numbers:
    • 0.5, π, 3.7, \( \sqrt{3} \), 2, \( \sqrt{7} \), 6.25, \( \sqrt{\dfrac{5}{2}} \), \( 3\dfrac{1}{4} \)

Answers

  1. 2.25, 2.65, \( 2\dfrac{1}{3} \), 2,75, 2,95
  2. 0.5, 3.7, 2, 6.25, \( 3\dfrac{1}{4} \)

Fractions

From Level 1 you are aware that fractions can be written as proper, improper and mixed fractions. Just like any other type of real numbers you should be able to add, subtract, multiply and divide fractions.

Addition and subtraction of fractions

When adding and subtracting fractions, put the fractions under a common denominator. If the fractions are mixed change them to improper fractions first. Now, look at the examples given below.

Example 1
Questions

  • Evaluate each of the following and write the answers as a fraction in its lowest terms.
    1. \( \dfrac{3}{5} + \dfrac{2}{7} \)
    2. \( \dfrac{3}{5} - \dfrac{2}{7} \)
    3. \( 6\dfrac{1}{5} - 2\dfrac{3}{4} + 1\dfrac{1}{6} \)

Answers

  1. \( \dfrac{3}{5} + \dfrac{2}{7} \\ = \dfrac{3 \times 7 + 2 \times 5}{35} \\ = \dfrac{21 + 10}{35} \\ = \dfrac{31}{35} \)
  2. \( \dfrac{3}{5} - \dfrac{2}{7} \\ = \dfrac{3 \times 7 - 2 \times 5}{35} \\ = \dfrac{21 - 10}{35} \\ = \dfrac{11}{35} \)
  3. \( 6\dfrac{1}{5} - 2\dfrac{3}{4} + 1\dfrac{1}{6} \\ = \dfrac{31}{5} - \dfrac{11}{4} + \dfrac{7}{6} \\ = \dfrac{31 \times 12 - 11 \times 15 + 7 \times 10}{60} \\ = \dfrac{277}{60} \\ = 4\dfrac{37}{60} \)

Hint: You are advised to change mixed numbers to improper fractions first.

Multiplication of fractions

When multiplying fractions, you start by multiplying the numerators on their own, do the same with the denominators and simplify to its lowest terms.

Example 2
Questions

  • Evaluate the following.
    1. \( \dfrac{3}{5} \times \dfrac{2}{7} \)
    2. \( \dfrac{7}{9} \times \dfrac{3}{5} \)

Answers

  1. \( \dfrac{3}{5} \times \dfrac{2}{7} \\ = \dfrac{3 \times 2}{5 \times 7} \\ = \dfrac{6}{35} \)
  2. \( \dfrac{7}{9} \times \dfrac{3}{5} \\ = \dfrac{7 \times 3}{9 \times 5} \\ = \dfrac{21}{45} \\ = \dfrac{7}{15} \)

Division of fractions

Dividing fractions is the same as multiplying by the reciprocal. The reciprocal of a number is obtained when 1 is divided by the number. For example, the reciprocal of 4 is \( \dfrac{1}{4} \), and the reciprocal of \( \dfrac{3}{5} \) is \( \dfrac{5}{3} \).

Example 3
Questions

  1. Find the reciprocal of the following.
    1. 6
    2. \( \dfrac{5}{8} \)
    3. \( \dfrac{3}{4} \)
    4. \( 1\dfrac{1}{2} \)
  2. Evaluate the following.
    1. \( \dfrac{5}{8} \div \dfrac{3}{7} \)
    2. \( \dfrac{3}{5} \div \dfrac{2}{3} \)

Answers

    1. \( \dfrac{1}{6} \)
    2. \( \dfrac{8}{5} \)
    3. \( \dfrac{4}{3} \)
    4. \( \dfrac{2}{3} \)
    1. \( \dfrac{5}{8} \div \dfrac{3}{7} \\ = \dfrac{5}{8} \times \dfrac{7}{3} \\ = \dfrac{35}{24} \\ = 1\dfrac{11}{24} \)
    2. \( \dfrac{3}{5} \div \dfrac{2}{3} \\ = \dfrac{3}{5} \times \dfrac{3}{2} \\ = \dfrac{9}{10} \)

Hint: When dividing fractions, you change the division sign to a multiplication sign then invert the second fraction.

You may attempt the following exercise.

Exercise 1.2: Fractions
Questions

  • Simplify the following.
    1. \( 4\dfrac{3}{5} - 1\dfrac{5}{8} \)
    2. \( 3\dfrac{1}{7} + 1\dfrac{2}{3} \)
    3. \( 9\dfrac{1}{3} + 5\dfrac{3}{4} - 6\dfrac{1}{2} \)
    4. \( 4\dfrac{1}{3} \times 2\dfrac{2}{5} \)
    5. \( 1\dfrac{1}{9} \div 1\dfrac{1}{3} \times 3\dfrac{3}{5} \)

Answers

  1. \( 2\dfrac{39}{40} \)
  2. \( 4\dfrac{17}{21} \)
  3. \( 8\dfrac{7}{12} \)
  4. \( 10\dfrac{2}{5} \)
  5. 3

Decimal numbers

Decimal numbers are numbers with a comma. Just like any other type of real numbers you should be able to add, subtract, multiply and divide decimal numbers.

Addition and Subtraction of Decimal Numbers

When adding and subtracting decimal numbers, you arrange the numbers in such a way that the commas are in a straight line downwards. Check this in the following worked example.

Example 4
Questions

  • Evaluate the following.
    1. 20.05 + 0.5
    2. 88.6 - 8.65
    3. 43.012 + 3.57 - 6.078

Answers

  1. \( \begin{array}{r}20.05 \\ + 0.50 \\ \hline 20.55 \\ \hline \end{array} \)
  2. \( \begin{array}{r}88.60 \\ - 8.65 \\ \hline 79.95 \\ \hline \end{array} \)
  3. \( \begin{array}{r}43.012 \\ + 3.570 \\ \hline 46.582 \\ - 6.078 \\ \hline 40.504 \\ \hline \end{array} \)

Multiplication of decimal numbers

When multiplying decimal numbers, ignore the comma, multiply as whole numbers and put the comma in the final answer as determined by the sum of decimal places in the numbers being multiplied.

Example 5
Questions

  • Evaluate the following.
    1. 6.05 × 0.25
    2. 4.15 × 0.013

Answers

  1. 6.05 × 0.25 = 1.5125. Calculate 605 × 25 = 15125, then count the decimal places.
  2. 4.15 × 0.013 = 0.05395. Calculate 415 × 13 = 5395, then count the decimal places.

Division of Decimal Numbers

When dividing decimal numbers make the denominator a whole number by multiplying by 10, 100 or 1000 depending on the number of decimal places in the denominator.

Example 6
Questions

  • Evaluate the following.
    1. 0.25 ÷ 0.125
    2. 0.05 ÷ 0.5
    3. 0.0216 ÷ 0.02

Answers

  1. \( 0.25 \div 0.125 \\ = \dfrac{0.25}{0.125} \times \dfrac{1000}{1000} \\ = \dfrac{250}{125} \\ = 2 \)
  2. \( 0.05 \div 0.5 \\ = \dfrac{0.05}{0.5} \times \dfrac{10}{10} \\ = \dfrac{0.5}{5} \\ = 0.1 \)
  3. \( 0.0216 \div 0.02 \\ = \dfrac{0.0216}{0.02} \times \dfrac{100}{100} \\ = \dfrac{2.16}{2} \\ = 1.08 \)

You may attempt the following exercise.

Exercise 1.3: Decimals
Questions

  1. Simplify the following.
    1. 3.73 + 93.68 − 7.30
    2. 6.32 × 3.4
    3. 0.0318 ÷ 0.003
    4. \( 0.3^3 \times 0.25 \div 0.04^2 \)
  2. During a cyclone, 0.6 of the cattle in a village were destroyed and only 240 cattle survived. How many cattle were in the village before the cyclone?

Answers

    1. 90.11
    2. 21.488
    3. 10.6
    4. 4.21875
  2. 600

Percentages

Percentage refers to the amount, number or rate of something, regarded as part of a total of 100. Percentages are fractions whose denominator is 100. For instance \( \dfrac{85}{100} \) can be written as 85%. Let us go through the following examples on how percentages are calculated.

Example 7
Questions

  1. Out of 50 learners in a class, 30 are girls and 20 are boys.
    1. What percentage of learners are girls?
    2. What percentage of learners are boys?
  2. Convert the following percentages to fractions and decimals.
    1. 23%
    2. 5%
  3. Convert the following to percentages.
    1. \( \dfrac{5}{8} \)
    2. 0.35

Answers

    1. \( \dfrac{30}{50} \times \dfrac{100}{1} \\ = \dfrac{3}{5} \times \dfrac{100}{1} \\ = 60\% \)
    2. \( \dfrac{20}{50} \times \dfrac{100}{1} \\ = \dfrac{2}{5} \times \dfrac{100}{1} \\ = 40\% \)
    1. \( \dfrac{23}{100} \\ = 0.23 \)
    2. \( \dfrac{5}{100} \\ = 0.05 \)
    1. \( \dfrac{5}{8} \times \dfrac{100}{1} \\ = 62.5\% \)
    2. \( 0.35 \\ = \dfrac{35}{100} \\ = 35\% \)

Calculating a percentage of a quantity

You might need to give 10% of your money to your friend. How then can you calculate the amount of money you will give to your friend? The following examples will illustrate how this is done.

Example 8
Questions

  • Evaluate the following.
    1. 10% of $80
    2. 25% of 200 meters

Answers

  1. \( \dfrac{10}{100} \times \dfrac{$80}{1} \\ = $8 \)
  2. \( \dfrac{25}{100} \times \dfrac{200 \ meters}{1} \\ = 50 \ meters \)

Expressing one quantity as a percentage of another

When expressing one quantity as a percentage of another, you first write the first quantity as a fraction of the second and then multiply by 100. Let’s now consider the following examples.

Example 9
Questions

  • Express the results of Learner A and Learner B as a percentage.
    1. Learner A got 15 out of 60
    2. Learner B got 50 out of 60

Answers

  1. \( \dfrac{15}{60} \times \dfrac{100}{1} \\ = 25\% \)
  2. \( \dfrac{50}{60} \times \dfrac{100}{1} \\ = 83.3\% \)

Percentage increases and decreases

Suppose you are working in a company earning $10,000 per month and your salary is to be increased by 20%. Use the space provided to calculate your new salary.

Example 10
Questions

  1. A shop assistant has a salary of $10,000 per month. If her salary is increased by 20%, calculate
    1. The extra amount she will receive a month.
    2. Her new monthly salary.
  2. A garage increases the price of fuel by 40%. If the original price was $9, calculate its new price.
  3. A rural shop is having a sale. They are selling a pair of shoes costing $75 at a 25% discount. Calculate the sale price of the pair of shoes.

Answers

    1. Increase = 20% of $10000.
      \( = \dfrac{20}{100} \times \dfrac{$10000}{1} \\ = $2000 \)
    2. New Salary = Old salary + Increase
      = $10000 + $2000 = $12000
  2. The original price represents 100%, therefore the new price represents 140%. New price = 140% of $9.
    \( = \dfrac{140}{100} \times \dfrac{$9}{1} \\ = 1.4 \times$9 \\ = $12.60 \)
  3. The old price represents 100%, therefore the new price can be represented as (100 – 25) % = 75%.
    \( = 75\% \ of \ $75 \\ = \dfrac{75}{100} \times \dfrac{$75}{1} = $56.25 \)

You may attempt the following exercise.

Exercise 1.4: Percentage increases and decreases
Questions

  • The marked price of a shirt in a shop is $75. A discount of 25% is given for cash payment.
    1. If Mr. Kamota paid cash. How much did he pay for the shirt?
    2. Mrs. Pindani, a flea market vendor bought 12 such shirts for cash. She went on to sell the shirts at $85 each. Calculate her profit.
    3. The marked price of $75 of the shirt had risen by 20% from that of last year. Calculate the price of the shirt last year.

Answers

  1. $56.25
  2. $345
  3. $62.50

1.3. Ratios, rates and proportions

Ratios

Ratios are used to compare related quantities. The simplest form of writing a ratio is a:b:c where a, b and c are whole numbers. Ratios can also be given as fractions, for example \( 1\dfrac{2}{3} \), and this has to be simplified by multiplying by the common denominator, which is 3 in this case, to give 3:2.

Example 11
Questions

  1. When cooking rice, usually 1 cup of rice is mixed with 2 cups of water. What is the ratio of rice to water?
  2. Ages of three family members are given as 18 years, 12 years and 3,6 years. Represent their ages as a ratio.
  3. A farmer has 80hectares of land. He would like to distribute the land in the ratio 3:2:5 for cultivating beans, maize and tobacco respectively. Calculate the size of land for each of the crops.

Answers

  1. The ratio is 1:3.
  2. The ages can be written as a ratio as 18years:12years:3.6years, which can be simplified to 18:12:3.6. The decimal point can be removed by multiplying each number by 10. This gives 180:120:36, which can be further simplified by dividing by 12 to give 15:10:3.
  3. Total ratio = 3 + 2 + 5 = 10
    • Beans \( = \dfrac{3}{10} \times \dfrac{80}{1} \\ = 24 \ hectares \)
    • Maize \( = \dfrac{2}{10} \times \dfrac{80}{1} \\ = 16 \ hectares \)
    • Tobacco \( = \dfrac{5}{10} \times \dfrac{80}{1} \\ = 40 \ hectares \)

You may attempt the following exercise.

Exercise 1.5: Ratios
Questions

  1. Divide the following quantities in the given ratio.
    1. $100 in the ratio 5:3.
    2. 50km in the ratio 3:2.
  2. A factory produces cars in red, blue, white and green in the ratio 7:5:3:1. Out of a production of 32 000 cars, how many cars are
    1. Red.
    2. White.

Answers

    1. $62.5 : $37.5
    2. 30km : 20km
    1. 14000 cars are red.
    2. 6000 cars are white.

Rates

Rates are used to compare quantities that are not related for example distance and time, number of papers produced by a photocopying machine over a period of time.

Example 12
Questions

  1. A faulty Range Rover consumes 2 liters of petrol over a distance of 10km. Calculate the amount of petrol consumed over a distance of 200km.
  2. A grinding mill produces 20 bags of mealie-meal over a period of 2 hours. Calculate the number of bags produced in 3 hours.

Answers

  1. You may work the question like this:
    10km = 2 liters
    200km = x liters
    Number of liters
    \( = \dfrac{200km}{10km} \times \dfrac{2 \ liters}{1} \\ = 40 \ liters \)
  2. You may work the question like this:
    20 bags = 2 hours
    x bags = 3 hours
    Number of bags
    \( = \dfrac{3 \ hours}{2 \ hours} \times \dfrac{20 \ bags}{1} \\ = 30 \ bags \)

Proportions

Proportions are used to compare quantities or to share quantities.

Example 13
Questions

  • Three boys Mac, Tinashe and Tom are aged 12, 14 and 20 respectively. They would like to share 69 oranges in the ratio of their ages. Calculate how many oranges each one of them is going to get.

Answers

  • The ratio is 12:14:20 reduced to 6:7:10 by dividing each number by 2. Total share = 6 + 7 + 10 = 23.
    • Mac’s share
      \( = \dfrac{6}{23} \times \dfrac{69}{1} \\ = 18 \ oranges \)
    • Tinashe’s share
      \( = \dfrac{7}{23} \times \dfrac{69}{1} \\ = 21 \ oranges \)
    • Tom’s share
      \( = \dfrac{10}{23} \times \dfrac{69}{1} \\ = 30 \ oranges \)

1.4. Irrational numbers

An irrational number is a type of real number which cannot be represented as a simple fraction. It cannot be expressed in the form of a ratio. If N is irrational, then N is not equal to p/q where p and q are integers and q is not equal to 0, for example Pi(π), \( \sqrt{3} \). Numbers that do not have exact square roots are called surds, for example \( \sqrt{3} \), \( \sqrt{5} \), \( 3\sqrt{7} \). Surds are a subset of irrational numbers. Surds can be combined, for example \( \sqrt{20} \) can be written as \( \sqrt{4 \times 5} \) = \( \sqrt{4} \times \sqrt{5} \) = \( 2\sqrt{5} \).

From the following list, identify surds in the space provided.

  • \( \sqrt{2} \), \( 3\sqrt{11} \), \( \sqrt{16} \), \( \sqrt{1\dfrac{9}{16}} \), \( \sqrt{12} \)

Hint: Numbers without exact square roots are your answers.

Surds can be manipulated and simplified according to a number of rules.

  1. \( \sqrt{a} \times \sqrt{a} = a \)
  2. \( \sqrt{a} \times \sqrt{b} = \sqrt{ab} \)
  3. \( \sqrt{a} \div \sqrt{b} = \sqrt{\dfrac{a}{b}} \)

Simplifying surds

The square root of some numbers which are not prime numbers can be simplified. The square root of a number cannot be simplified when it is in its basic form.

Example 14
Questions

  • Simplify the following surds.
    1. \( \sqrt{20} \)
    2. \( \sqrt{27} \)
    3. \( \sqrt{12} \)

Answers

  1. \( \sqrt{20} = \sqrt{4 \times 5} \\ = \sqrt{4} \times \sqrt{5} \\ = 2\sqrt{5} \\ \)
  2. \( \sqrt{27} \\ = \sqrt{9 \times 3} \\ = \sqrt{9} \times \sqrt{3} \\ = 3\sqrt{3} \)
  3. \( \sqrt{12} \\ = \sqrt{4 \times 3} \\ = \sqrt{4} \times \sqrt{3} \\ = 2\sqrt{3} \)

Addition and subtraction of surds

In order for you to add or subtract surds, make sure numbers under the square root are the same.

Example 15
Questions

  • Evaluate the following where possible.
    1. \( 4\sqrt{3} + 2\sqrt{3} \)
    2. \( 4\sqrt{2} + 3\sqrt{5} \)
    3. \( 4\sqrt{3} - 2\sqrt{3} \)
    4. \( \sqrt{3} + \sqrt{12} \)

Answers

  1. \( 4\sqrt{3} + 2\sqrt{3} \). This can be taken as 4a + 2a = 6a, thus \( \sqrt{3} \) is taken as an unknown a, = \( 6\sqrt{3} \).
  2. \( 4\sqrt{2} + 3\sqrt{5} \). This cannot be added because the numbers below the \( \sqrt{} \) are not the same, this can be taken as 4c + 3d.
  3. \( 4\sqrt{3} - 2\sqrt{3} \). This can be taken as 4a - 2a = 2a, thus \( \sqrt{3} \) is taken as an unknown a, = \( 2\sqrt{3} \)
  4. \( \sqrt{3} + \sqrt{12} = \sqrt{3} + \sqrt{4 \times 3} = \sqrt{3} + \sqrt{4} \times \sqrt{3} = \sqrt{3} + 2 \times \sqrt{3} = \sqrt{3} + 2\sqrt{3} = 3\sqrt{3} \).

Multiplication of surds

To multiply surds, simply multiply the numbers outside of the square root sign together and then multiply the square roots together. Finally, simplify if possible. For example, \( a\sqrt{b} \times c\sqrt{d} = ac\sqrt{bd} \).

Example 16
Questions

  • Evaluate the following.
    1. \( \sqrt{3} \times \sqrt{2} \)
    2. \( \sqrt{3} \times \sqrt{3} \)
    3. \( 3\sqrt{2} \times 4\sqrt{5} \)

Answers

  1. \( \sqrt{3} \times \sqrt{2} = \sqrt{3 \times 2} = \sqrt{6} \)
  2. \( \sqrt{3} \times \sqrt{3} = \sqrt{3 \times 3} = \sqrt{9} = 3 \)
  3. \( 3\sqrt{2} \times 4\sqrt{5} = 3 \times 4 \times \sqrt{2} \times \sqrt{5} = 12\sqrt{10} \)

Division of surds

To divide surds, divide the whole numbers outside of the square root sign by each other and then divide the square roots by each other. Finally, simplify if possible. For example, \( a\sqrt{b} \div c\sqrt{d} = \dfrac{a}{c}\sqrt{\dfrac{b}{d}} \).

To divide surds, you can also multiply both the numerator and the denominator by the denominator, a process known as rationalisation of the denominator.

Example 17
Questions

  • Rationalise the following.
    1. \( \dfrac{2}{\sqrt{3}} \)
    2. \( \dfrac{3}{\sqrt{5}} \)

Answers

  1. \( \dfrac{2}{\sqrt{3}} \). Multiply both numerator and denominator by \( \sqrt{3} \).
    \( = \dfrac{2}{\sqrt{3}} \times \dfrac{\sqrt{3}}{\sqrt{3}} \\ = \dfrac{2\sqrt{3}}{\sqrt{3} \times \sqrt{3}} \\ = \dfrac{2\sqrt{3}}{\sqrt{3 \times 3}} \\ = \dfrac{2\sqrt{3}}{\sqrt{9}} \\ = \dfrac{2\sqrt{3}}{3} \)
  2. \( \dfrac{3}{\sqrt{5}} \). Multiply both numerator and denominator by \( \sqrt{5} \).
    \( = \dfrac{3}{\sqrt{5}} \times \dfrac{\sqrt{5}}{\sqrt{5}} \\ = \dfrac{3\sqrt{5}}{\sqrt{5} \times \sqrt{5}} \\ = \dfrac{3\sqrt{5}}{\sqrt{5 \times 5}} \\ = \dfrac{3\sqrt{5}}{\sqrt{25}} \\ = \dfrac{3\sqrt{5}}{5} \)

You may attempt the following exercise.

Exercise 1.6: Surds
Questions

  • Simplify the following.
    1. \( 5\sqrt{12} + 2\sqrt{3} \)
    2. \( 4\sqrt{2} - \sqrt{18} \)
    3. \( \sqrt{3} \times \sqrt{5} \)
    4. \( \dfrac{4}{\sqrt{3}} \)
    5. \( \sqrt{3} + \dfrac{1}{\sqrt{3}} - \dfrac{1}{\sqrt{27}} \)
    6. \( 5\sqrt{2} - 3\sqrt{8} \)
    7. \( 3\sqrt{28} - \sqrt{7} \)
    8. \( (2 + \sqrt{3})(4 + \sqrt{3}) \)
    9. \( (2 + \sqrt{3})(2 - \sqrt{3}) \)
    10. \( \dfrac{4 + \sqrt{3}}{2 - \sqrt{3}} \). Hint: Multiply both numerator and denominator by \( (2 + \sqrt{3}) \).

Answers

  1. \( 12\sqrt{3} \)
  2. \( \sqrt{2} \)
  3. \( \sqrt{15} \)
  4. \( \dfrac{4\sqrt{3}}{3} \)
  5. \( \dfrac{11\sqrt{3}}{9} \)
  6. \( - \sqrt{2} \)
  7. \( 5\sqrt{2} \)
  8. \( 11 + 6\sqrt{3} \)
  9. 1
  10. \( 11 + 6\sqrt{3} \)

1.5. Approximations, estimations and limits of accuracy

When shopping groceries, you sometimes estimate the amount you are going to pay at the till. An estimate gives a rough idea of how much you are going to pay. Approximations and estimations are usually done using place values, decimal places and significant figures.

Place values

Given a number like 4975.683 from your Level 1 you established that every digit in this number has a place value for example 6 is a tenth. Let us look at rounding of numbers using place values.

Example 18
Questions

  • Round off 74.685 to the nearest
    1. Tenth
    2. Hundredth
    3. Ten
    4. Whole number

Answers

  1. 74.7. Note that the tenth value we are interested in is 6, we look at the number 6, if it’s below 5 we round down and when it’s 5 and above we round up.
  2. 74.69
  3. 70
  4. 75

Decimal places

Hope you are familiar with decimal places from your level 1. Decimal places are the number of digits after the comma. For instance 50.697 has 3 decimal places.

Example 19
Questions

  • Round off the number 5.545 to
    1. 1 decimal place
    2. 2 decimal place
    3. 3 decimal place

Answers

  1. 5.5
  2. 5.55
  3. 5.545

Significant figures (s.f.)

Numbers can also be rounded off using significant figures. Significant figures are counted from the first non-zero digit. The number 0.0407 has 3 significant figures, that is, 4, 0 and 7. The first 2 zeros are place holders.

Example 20
Questions

  1. Round off the number 0.008046 to
    1. 1 s.f.
    2. 2 s.f.
    3. 3 s.f.
  2. Round off the number 475.063 to
    1. 1 s.f.
    2. 2 s.f.
    3. 3 s.f.
    4. 4 s.f.
    5. 5 s.f.

Answers

    1. 0.008
    2. 0.0080
    3. 0.00805
    1. 500
    2. 480
    3. 475
    4. 475.1
    5. 475.06

Estimations

Any answer for a given question can be given as an approximate solution and it is called an estimate.

Example 21
Questions

  1. Estimate each number to 1 s.f. and evaluate the following.
    1. 23 × 34
    2. 0.8 × 4.75
    3. 70.45 + 51.05
    4. 168.3 + 42.08
    5. 123 – 77
    6. 346.40 – 298.89
  2. By first rounding off each number to the nearest whole number, estimate the value of \( \dfrac{7.03 \times 19.8 - 8.47}{10.84} \).

Answers

    1. 23 × 34 = 20 × 30 = 600
    2. 0.8 × 4.75 = 0.8 × 5 = 4
    3. 70.45 + 51.05 = 70 + 50 = 120
    4. 168.3 + 42.08 = 200 + 40 = 24
    5. 123 – 77 = 120 – 80 = 40
    6. 346.40 – 298.89 = 300 – 300 = 0
  2. \( \dfrac{7.03 \times 19.8 - 8.47}{10.84} \\ = \dfrac{7 \times 20 - 8}{11} \\ = \dfrac{140 - 8}{11} \\ = \dfrac{132}{11} \\ = 12 \)

Limits of accuracy

ln most cases we tend to give our ages as whole numbers. We rarely give our ages as 24 years 2 months 3 weeks but we just say 24 years old.

Example 22
Questions

  • Chipo is asked her age and she gives her age as 17 years to the nearest whole number. What are the limits of her age?

Answers

  • Limits give us the smallest and the greatest number that can be rounded off to 17 years. The lower limit is 16.5 and the upper limit is greatest value less than 17.5 as illustrated on the diagram below.

Figure 1.1

The answer is given as an inequality 16.5 ≤ A < 17.5 where A is the approximate age.

Example 23
Questions

  • The sides of a square are given as 3.8cm to 1 decimal place.
    1. Write down the limits of the length of the sides of the square in the form a ≤ L < b.
    2. Hence calculate the least possible perimeter of the square.

Answers

  1. The lower limit is 3.75 and the upper limit is 3.85 as illustrated on the diagram below

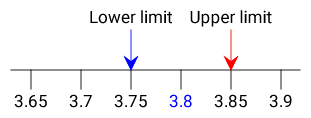
    Figure 1.2

    3.75 ≤ L < 3.85
  2. Least possible perimeter (using the lower limit) is 3.75 × 4 = 15 cm.

You may attempt the following exercise.

Exercise 1.7: Rational and irrational numbers
Questions

  1. Express 0.04056 to
    1. 3 decimal places
    2. 2 significant figures
  2. Chipo gave her mass as 64kg to the nearest kg. Write down the limits of her mass in the form a ≤ m < b.
  3. By rounding each of the numbers to 1 significant figure, estimate the value of \( \dfrac{384 \div 486}{\sqrt{675 - 624}} \)

Answers

    1. 0.041
    2. 0.041
  2. 63.5 ≤ m < 64.5
  3. 0.05

1.6. Ordinary and standard form

In life we have very small and very large numbers, for instance the size of a virus or the distance between the sun and the earth. Such numbers are best understood if they are written in standard form. Standard form is also known as standard index form or sometimes as scientific notation. It involves writing large numbers or very small numbers in terms of powers of 10.

Large numbers

Generally when a number is in standard form it should be written in the form \( A \times 10^n \) where A is a number between 1 and 10 thus 1 ≤ A < 10. The number 2700 can be written in different ways: \( 27 \times 10^2 \), \( 2.7 \times 10^3 \), \( 270 \times 10^1 \), \( 2700 \times 10^0 \) etc. However, \( 2.7 \times 10^3 \) is the only one in standard form since it agrees with the above condition that 1 ≤ A < 10.

Example 24
Questions

  • Represent the following ordinary numbers in standard form.
    1. 9000
    2. 43000
    3. 47.689
    4. 84670

Answers

  1. \( 9000 \\ = 9 \times 1000 \\ = 9 \times 10^3 \)
  2. \( 43000 \\ = 4.3 \times 10000 \\ = 4.3 \times 10^4 \)
  3. \( 47.689 \\ = 4.7689 \times 10 \\ = 4.7689 \times 10^1 \)
  4. \( 84670 \\ = 8.467 \times 10000 \\ = 8.467 \times 10^4 \)

Ordinary form

You should be able to change a number in standard back to its ordinary from.

Example 25
Questions

  • Express the following numbers in ordinary form.
    1. \( 4.37 \times 10^3 \)
    2. \( 8 \times 10^{-3} \)
    3. \( 4.37 \times 10^{-3} \)
    4. \( 4.365 \times 10^{-1} \)
    5. \( 4.37 \times 10^{-9} \)

Answers

  1. \( 4.37 \times 10^3 \\ = 4.37 \times 1000 = 4370 \)
  2. \( 8 \times 10^{-3} \\ = 8 \times \dfrac{1}{10^3} \\ = \dfrac{8}{10^3} \\ = \dfrac{8}{1000} \\ = 0.008 \)
  3. \( 4.37 \times 10^{-3} \\ = 4.37 \times \dfrac{1}{10^3} \\ = \dfrac{4.37}{10^3} \\ = \dfrac{4.37}{1000} \\ = 0.00437 \)
  4. \( 4.365 \times 10^{-1} \\ = 4.365 \times \dfrac{1}{10^1} \\ = \dfrac{4.365}{10^1} \\ = \dfrac{4.365}{10} \\ = 0.04365 \)
  5. \( 4.37 \times 10^{-9} \\ = 4.37 \times \dfrac{1}{10^9} \\ = \dfrac{4.37}{10^9} \\ = \dfrac{4.37}{1000000000} \\ = 0.00000000437 \)

Addition and subtraction of numbers in standard form

Numbers in standard form can be added or subtracted. There are two methods of adding and subtracting numbers in standard form:

  1. Changing to ordinary
  2. Factorisation

Example 26
Questions

  • Simplify the following leaving your answer in standard form.
    1. \( 3.8 \times 10^3 + 4.17 \times 10^4 \)
    2. \( 4.37 \times 10^4 - 2.3 \times 10^3 \)
    3. \( 4.8 \times 10^{-3} - 2.3 \times 10^{-3} \)

Answers

  1. Method 1: By changing to ordinary form
    \( 3.8 \times 10^3 + 4.17 \times 10^4 \\ = 3.8 \times 1000 + 4.17 \times 10000 \\ = 3800 + 41700 = 45500 = 4.55 \times 10^4 \)
    Method 2: By factorisation
    \( 3.8 \times 10^3 + 4.17 \times 10^4 \)
    Identify a common factor and write it outside the brackets:
    \( = 10^3(3.8 + 4.17 \times 10) \\ = 10^3(3.8 + 41.7) \\ = 10^3(45.5) \\ = 45.5 \times 10^3 \)
    45.5 is not between 1 and 10 so change it to standard form.
    \( = 4.55 \times 10^1 \times 10^3 \\ = 4.55 \times 10^4 \)
  2. Method 1: By changing to ordinary form
    \( 4.37 \times 10^4 - 2.3 \times 10^3 \\ = 4.37 \times 10000 - 2.3 \times 1000 \\ = 43700 - 2300 = 41400 = 4.14 \times 10^4 \)
    Method 2: By factorisation
    \( 4.37 \times 10^4 - 2.3 \times 10^3 \)
    Identify a common factor and write it outside the brackets:
    \( = 10^3(4.37 \times 10 - 2.3) \\ = 10^3(43.7 - 2.3) \\ = 10^3(41.4) \\ = 41.4 \times 10^3 \\ \)
    41.4 is not between 1 and 10 so change it to standard form.
    \( = 4.14 \times 10^1 \times 10^3 \\ = 4.14 \times 10^4 \)
  3. Method 1: By changing to ordinary form
    \( 4.8 \times 10^{-3} - 2.3 \times 10^{-3} \\ = 4.8 \times 0.001 - 2.3 \times 0.001 \\ = 0.0048 - 0.0023 \\ = 0.0025 = 2.5 \times 10^{-3} \)
    Method 2: By factorisation
    \( 4.8 \times 10^{-3} - 2.3 \times 10^{-3} \)
    Identify a common factor and write it outside the brackets:
    \( = 10^{-3}(4.8 - 2.3) \\ = 10^{-3}(2.5) \\ = 2.5 \times 10^{-3} \)

Multiplication and division of numbers in standard form

When multiplying and dividing numbers in standard form multiply and divide like terms. For example, \( a \times 10^x \times b \times 10^y = a \times b \times 10^x \times 10^y \).

Example 27
Questions

  • Simplify the following.
    1. \( 6 \times 10^4 \times 7 \times 10^5 \)
    2. \( \dfrac{4.2 \times 10^{-3}}{2.1 \times 10^{-4}} \)

Answers

  1. \( 6 \times 10^4 \times 7 \times 10^5 \\ = 6 \times 7 \times 10^4 \times 10^5 \\ = 42 \times 10^{4 + 5} \\ = 42 \times 10^9 \\ = 4.2 \times 10^1 \times 10^9 \\ = 4.2 \times 10^{10} \)
  2. \( \dfrac{4.2 \times 10^{-3}}{2.1 \times 10^{-4}} \\ = \dfrac{4.2}{2.1} \times \dfrac{10^{-3}}{10^{-4}} \\ = 2 \times 10^{- 3 -(- 4)} \\ = 2 \times 10^{- 3 + 4} \\ = 2 \times 10^1 \)

You may attempt the following exercise.

Exercise 1.8: Ordinary and standard form
Questions

  1. Express the following numbers in standard form.
    1. 472
    2. 0.472
    3. 0.0057
    4. 0.00000483
    5. 38.043
  2. Write the following in ordinary form.
    1. \( 5.31 \times 10^3 \)
    2. \( 5.31 \times 10^{-3} \)
  3. Given that \( a = 4.2 \times 10^3 \) and \( b = 2.1 \times 10^2 \). Find
    1. a + b
    2. a - b
    3. ab
    4. \( \dfrac{a}{b} \)
    5. \( a^2 \)

Answers

    1. \( 4.72 \times 10^2 \)
    2. \( 4.72 \times 10^{-1} \)
    3. \( 5.7 \times 10^{-3} \)
    4. \( 4.83 \times 10^{-6} \)
    5. \( 3.8043 \times 10^1 \)
    1. 5310
    2. 0.00531
    1. \( 4.41 \times 10^3 \)
    2. \( 3.99 \times 10^3 \)
    3. \( 8.82 \times 10^5 \)
    4. \( 2 \times 10^1 \)
    5. \( 1.764 \times 10^7 \)

1.7. Number bases

Given that a number like 4784 can be written as:

  • 4000 + 700 + 80 + 4, or
  • \( 4 \times 10^3 + 7 \times 10^2 + 8 \times 10^1 + 4 \times 10^0 \).

4784 has been given in expanded form as a base of 10, so 4784 can be written as:

  • \( 4784_{ten} \) or \( 4784_{10} \)

Ordinary numbers that we deal with everyday are in base 10 (denary base). Numbers can be converted from one base to another, that is, they can be converted from base 10 to bases 2, 3, 4, 5, 6, 7, 8 or 9 and vise versa.

Expanding numbers in a given base

Let us look at expanding numbers in a given base.

Example 28
Questions

  • Expand the following.
    1. \( 5632_{10} \)
    2. \( 10111_{2} \)
    3. \( 43211_{5} \)

Answers

  1. \( 5632_{10} \\ = 5 \times 10^3 + 6 \times 10^2 + 3 \times 10^1 + 2 \times 10^0 \)
  2. \( 10111_{2} \\ = 1 \times 2^4 + 0 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 \)
  3. \( 43211_{5} \\ = 4 \times 5^4 + 3 \times 5^3 + 2 \times 5^2 + 1 \times 5^1 + 1 \times 5^0 \)

Converting numbers in base 10 to any other base

You should be able to convert a number in base 10 to any other base.

Example 29
Questions

  • Convert \( 47_{10} \) to base
    1. 2
    2. 5
    3. 8

Answers

  1. \( 47_{10} \) to base 2 (divide 47 by 2 and take the remainders from bottom upwards):
    \( \begin{array}{r}2 \ | 47 \ \phantom{0} \ \phantom{0} \\ 2 \ | 23 \ r \ 1 \\ 2 \ | 11 \ r \ 1 \\ 2 \ | \phantom{0}5 \ r \ 1 \\ 2 \ | \phantom{0}2 \ r \ 1 \\ 2 \ | \phantom{0}1 \ r \ 0 \\ \phantom{0} \ \phantom{0}0 \ r \ 1 \end{array} \)
    \( = 101111_{2} \)
  2. \( 47_{10} \) to base 5 (divide 47 by 5 and take the remainders from bottom upwards):
    \( \begin{array}{r}5 \ | 47 \ \phantom{0} \ \phantom{0} \\ 5 \ | \phantom{0}9 \ r \ 2 \\ 5 \ | \phantom{0}1 \ r \ 4 \\ \phantom{0} \ \phantom{0}0 \ r \ 1 \end{array} \)
    \( = 142_{5} \)
  3. \( 47_{10} \) to base 8 (divide 47 by 8 and take the remainders from bottom upwards):
    \( \begin{array}{r}8 \ | 47 \ \phantom{0} \ \phantom{0} \\ 8 \ | \phantom{0}5 \ r \ 7 \\ \phantom{0} \ \phantom{0}0 \ r \ 5 \end{array} \)
    \( = 57_{8} \)

Converting from any base to base 10

When converting a number to base 10, you expand the number and simplify.

Example 30
Questions

  • Expand and convert the following to base 10.
    1. \( 142_{5} \)
    2. \( 3201_{4} \)
    3. \( 101111_{2} \)

Answers

  1. \( 142_{5} = 1 \times 5^2 + 4 \times 5^1 + 2 \times 5^0 \\ = 25 + 20 + 2 = 47_{10} \)
  2. \( 3201_{4} = 3 \times 4^3 + 2 \times 4^2 + 0 \times 4^1 + 1 \times 4^0 \\ = 192 + 32 + 0 + 1 = 225_{10} \)
  3. \( 101111_{2} = 1 \times 2^5 + 0 \times 2^4 + 1 \times 2^3 + 1 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 32 + 0 + 8 + 4 + 2 + 1 = 47_{10} \)

Converting from any base to another base

When changing a number that is not in base 10, for instance from base 2 to base 5, you need to pass through base 10.

Example 31
Questions

  • Convert \( 11011_{2} \) to base 5

Answers

  • First convert to base 10 (expand)
    \( 11011_{2} \\ = 1 \times 2^4 + 1 \times 2^3 + 0 \times 2^2 + 1 \times 2^1 + 1 \times 2^0 = 16 + 8 + 0 + 2 + 1 = 27_{10} \)
    Then convert to base 5 (simplify)
    \( \begin{array}{r}5 \ | 27 \ \phantom{0} \ \phantom{0} \\ 5 \ | \phantom{0}5 \ r \ 2 \\ 5 \ | \phantom{0}1 \ r \ 0 \\ \phantom{0} \ \phantom{0}0 \ r \ 1 \end{array} \)
    \( = 102_{5} \)

Addition and subtraction of numbers in bases

You have observed from previous examples that when a number is in base 2, it only has ones and zeros, that is, it has digits less than 2. Also, a number in base 5 has digits less than 5.

Example 32
Questions

  • Evaluate \( 434_{5} + 423_{5} \) giving your answer in base 5.

Answers

  • Method 1
    \( 434_{5} + 423_{5} \)
    \( \begin{array}{r}\phantom{+}434_{5} \\ + 423_{5} \\ \hline 1412_{5} \\ \hline \end{array} \)
    Step 1: 4 + 3 = 7, divide 7 by 5 = 1 r 2, put down the remainder 2 and carry 1.
    Step 2: 3 + 2 + 1 = 6, divide 6 by 5 = 1 r 1, put down the remainder 1 and carry 1.
    Step 3: 4 + 4 + 1 = 9, divide 9 by 5 = 1 r 4, put down the remainder 4 and carry 1.
    Method 2
    \( 434_{5} + 423_{5} \)
    Step 1: Convert to base 10
    \( 434_{5} \) to base 10
    \( = 4 \times 5^2 + 3 \times 5^1 + 4 \times 5^0 \\ = 100 + 15 + 4 \\ = 119_{10} \)
    \( 423_{5} \) to base 10
    \( = 4 \times 5^2 + 2 \times 5^1 + 3 \times 5^0 \\ = 100 + 10 + 3 \\ = 113_{10} \)
    Step 2: Add the numbers in base 10
    \( 434_{5} + 423_{5} \\ = 119_{10} + 113_{10} \\ = 232_{10} \)
    Step 3: Convert the sum to base 5
    \( \begin{array}{r}5 \ | 232 \ \phantom{0} \ \phantom{0} \\ 5 \ | \phantom{0}46 \ r \ 2 \\ 5 \ | \phantom{00}9 \ r \ 1 \\ 5 \ | \phantom{00}1 \ r \ 4 \\ \phantom{0} \ \phantom{0}0 \ r \ 1 \end{array} \)
    \( = 1412_{5} \)

Note: Method 2 is suitable when adding and subtracting numbers that have different bases.

Example 33
Questions

  1. \( 4312_{5} - 434_{5} \)

Answers

  1. \( 4312_{5} - 434_{5} \)
    \( \begin{array}{r}4312_{5} \\ - 434_{5} \\ \hline 3323_{5} \\ \hline \end{array} \)
    Step 1: 2 – 4 is not possible, so add 5 to 2 to get 7, then 7 – 4 = 3, write 3.
    Step 2: Add 1 to 3 to get 4, but 1 – 4 is not possible, so add 5 to 1, to get 6 – 4 = 2, write 2.
    Step 3: Add 1 to 4 to get 5, but 3 – 5 is not possible, so add 5 to 3, to get 8 – 5 = 3, write 3.
    Step 4: Add 1 to 0 to get 1, then 4 – 1 = 3, then write 3.

Alternatively, you can subtract by first changing the numbers to base 10. Try the process until you get the answer \( 3323_{5} \).

You may attempt the following exercise.

Exercise 1.9: Number bases
Questions

  1. Convert \( 97_{10} \) to
    1. base 5
    2. base 8
  2. Convert the following numbers to base 10.
    1. \( 4112_{5} \)
    2. \( 413_{8} \)
  3. Convert
    1. \( 213_{5} \) to base 2
    2. \( 416_{8} \) to base 5
  4. Solve. (Hint: Give answer in base 10)
    1. \( 413_{5} + 143_{5} \)
    2. \( 1100_{2} - 111_{2} \)
    3. \( 431_{5} + 450_{6} \)

Answers

    1. \( 342_{5} \)
    2. \( 141_{8} \)
    1. \( 532_{10} \)
    2. \( 267_{10} \)
    1. \( 111010_{2} \)
    2. \( 2040_{5} \)
    1. \( 1111_{5} \)
    2. \( 101_{2} \)
    3. \( 290_{10} \)

1.8. Scale and simple map problems

Scale on maps and plans is given as a ratio in the form 1:n. For example 1:500 means 1cm represents 500cm or 1cm represents 5m. If on a map the scale is given as 1:50 000 that means 1cm represents 50 000cm therefore 1cm represents 500m, then 1cm represents 0.5km. The scale for length can be changed to become scale for area by squaring both sides. For instance if the scale for length is 2cm represents 5m then the scale for area becomes \( 4cm^2 \) represents \( 25m^2 \).

Example 34
Questions

  • The scale on a building plan is given as 1:500.
    1. Find the actual length of a window on the map that has length 8cm in metres.
    2. The actual length of the building is 30m. Find the length on the map.
    3. Area of one of the rooms of a house on the plan is \( 18cm^2 \). Find the actual area of the room in \( m^2 \).

Answers

  1. 1:500 means 1cm represents 500cm then 1cm represents 5m
    1cm represents 5m
    8cm represents ?
    \( \dfrac{8cm}{1cm} \times \dfrac{5m}{1} = 40m \)
  2. 5m represents 1cm
    30m represents ?
    \( \dfrac{30m}{5m} \times \dfrac{1cm}{1} = 6cm \)
  3. Scale for area
    \( (1cm)^2 \) represents \( (5m)^2 \)
    \( 1cm^2 \) represents \( 25m^2 \)
    \( 18cm^2 \) represents ?
    \( \dfrac{18cm^2}{1cm^2} \times \dfrac{25m^2}{1} = 450m^2 \)

You may attempt the following exercise.

Exercise 1.10: Scale and simple map problems
Questions

  • The scale on a map is given as 1cm represents 5km
    1. Write the scale in the form 1:n.
    2. If the distance between two towns Rusape and Mutare is 16cm on the map, find the actual distance between Rusape and Mutare in km.
    3. The area of an airport on a map is \( 12cm^2 \), calculate the actual area of the airport in \( km^2 \).

Answers

  1. 500000
  2. 80km
  3. \( 300km^2 \)

1.9. Number patterns and sequences

A sequence is a set of numbers which follows a well defined order or rule, for example 1, 2, 4, 8, 16,... or 2, 4, 6, 8, 10,...

Example 35
Questions

  1. Write the next 3 terms of the sequence 1, 3, 5, 7,...
  2. Write the next 3 terms of the sequence 2, 4, 8, 16,...

Answers

  1. 9, 11, 13. The sequence is a set of odd numbers obtained by adding 2.
  2. 32, 64, 128. The sequence is a set of numbers obtained by multiplying the previous number by 2.

1.10. Summary

From this chapter you have realised that different types of numbers can be added, subtracted, multiplied and divided differently. This chapter is acting as the basis of understanding the next chapters. You can also use the skills you have acquired in this chapter in other learning areas. If you have mastered the skills in this chapter then move on to the next chapter.

1.11. Further reading

  1. Macrae, M. F., Madungwe, L. and Mutangadura, A. (2017). New General Mathematics Book 3. Pearson Capetown.
  2. Macrae, M. F., Madungwe, L. and Mutangadura, A. (2017). New General Mathematics Book 4. Pearson Capetown.
  3. Meyers, C., Graham, B., Dawe, L. (2004). Mathscape Working Mathematically. 9th Edition. MacMillan.
  4. Pimentel, R. and Wall, T. (2011). International Mathematics. Hodder UK.
  5. Rayner, D. (2005). Extended Mathematics. Oxford New York.

1.12. Test 1

Answer the following questions. Do not use a calculator.

Questions

  1. Express 43786
    1. in standard form   [1]
    2. to the nearest thousand   [1]
    3. to three significant figures   [1]
  2. Write 0.085
    1. in standard form   [1]
    2. as a fraction in its lowest terms   [1]
    3. to two decimal places   [1]
  3. Evaluate
    1. \( 1\dfrac{3}{4} - \dfrac{2}{5} + 5\dfrac{1}{3} \)   [1]
    2. \( 0.06 \times 0.003 \)   [1]
    3. \( \dfrac{0.3^2 \times 0.2}{0.06} \)   [1]
    1. Write 3.65 hours in hours and minutes   [1]
    2. The price of a radio is $270. This price is 20% more than last year’s price. Calculate last year’s price of the radio.   [2]
    1. Write down the largest 4 -digit number in base 9   [1]
    2. Convert \( 412_{10} \) to base 8   [1]
    3. Convert \( 112_{10} \) to base 3   [1]
  6. Given that \( a = 9 \times 10^8 \), \( b = 6 \times 10^5 \). Find the value of
    1. a + b   [1]
    2. ab   [1]
    3. \( \sqrt{a} \)   [1]
    4. \( \dfrac{a}{b} \)   [1]
  7. The diameter of a circle is given as 9,4cm to 1 decimal place.
    1. Write down the limits of the diameter in the form a ≤ d < b.   [2]
    2. Calculate the least possible circumference of the circle in terms of π.   [2]
    1. Of the livestock on the farm, 70% are cattle and the rest are goats. If the farmer has 18 goats, calculate the total livestock on the farm.   [2]
    2. When making a concrete mixture of cement, sand and concrete the ratio 2:3:4 is used respectively. Calculate the number of wheelbarrows of sand required if there are 6 bags of cement.   [2]
  9. Tendai and Tanaka are 12 years and 30 years respectively.
    1. Write down their ages as a ratio in its simplest form in the form a:b.   [1]
    2. If they share some money in the ratio of their ages, and Tendai got $24. How much did Tanaka get?   [2]
  10. The scale on a map is given as 1:250.
    1. Calculate the actual length of a church building in metres if it is 8cm on the map.   [2]
    2. The area of a room on the map is \( 12cm^2 \). Calculate the actual area of the room in \( m^2 \).   [2]

Answers

    1. \( 4.3786 \times 10^4 \)
    2. 44000
    3. 43800
    1. \( 8.5 \times 10^{-2} \)
    2. \( \dfrac{17}{200} \)
    3. 0.09
    1. \( 6\dfrac{41}{60} \)
    2. 0.00018
    3. 0.3
    1. 3 hours 39 minutes
    2. $225
    1. 8888
    2. \( 634_{8} \)
    3. \( 1012_{3} \)
    1. \( 9.006 \times 10^8 \)
    2. \( 5.4 \times 10^{14} \)
    3. \( 1.5 \times 10^3 \)
    4. \( 3 \times 10^4 \)
    1. 9.35 ≤ d < 9.45
    2. 9.35π
    1. 60
    2. 9
    1. 2:5
    2. $60
    1. 20m
    2. \( 75m^2 \)